Image features¶
In this chapter we will describe a set of quantitative image features together with the reference values established by the IBSI. This feature set builds upon the feature sets proposed by [Aerts2014] and [Hatt2016], which are themselves largely derived from earlier works. References to earlier work are provided whenever they could be identified.
Reference values were derived for each feature. A table of reference values contains the values that could be reliably reproduced, within a tolerance margin, for the reference data sets (see Reference data sets). Consensus on the validity of each reference value is also noted. Consensus can have four levels, depending on the number of teams that were able to produce the same value during the standardization process: weak (\(<3\) matches), moderate (\(3\) to \(5\) matches), strong (\(6\) to \(9\) matches), and very strong (\(\geq 10\) matches). If consensus on a reference value was weak or if it could not be reproduced by an absolute majority of teams, it was not considered standardized. Such features do currently not have reference values, and should not be used.
The set of features can be divided into a number of families, of which intensity-based statistical, intensity histogram-based, intensity-volume histogram-based, morphological features, local intensity, and texture matrix-based features are treated here. All texture matrices are rotationally and translationally invariant. Illumination invariance of texture matrices may be achieved by particular image post-acquisition schemes, e.g. histogram matching. None of the texture matrices are scale invariant, a property which can be useful in many (biomedical) applications. What the presented texture matrices lack, however, is directionality in combination with rotation invariance. These may be achieved by local binary patterns and steerable filters, which however fall beyond the scope of the current work. For these and other texture features, see [Depeursinge2014].
Features are calculated on the base image, as well as images transformed using wavelet or Gabor filters). To calculate features, it is assumed that an image segmentation mask exists, which identifies the voxels located within a region of interest (ROI). The ROI itself consists of two masks, an intensity mask and a morphological mask. These masks may be identical, but not necessarily so, as described in the section on Re-segmentation.
Several feature families require additional image processing steps before feature calculation. Notably intensity histogram and texture feature families require prior discretisation of intensities into grey level bins. Other feature families do not require discretisation before calculations. For more details on image processing, see Fig. 1 in the previous chapter.
Below is an overview table that summarises image processing requirements for the different feature families.
| ROI mask | ||||
|---|---|---|---|---|
| Feature family | count | morph. | int. | discr. |
| morphology | 29 | ✔ | ✔ | ✕ |
| local intensity | 2 | ✕ | ✔ a | ✕ |
| intensity-based statistics | 18 | ✕ | ✔ | ✕ |
| intensity histogram | 23 | ✕ | ✔ | ✔ |
| intensity-volume histogram | 5 | ✕ | ✔ | ✔ b |
| grey level co-occurrence matrix | 25 | ✕ | ✔ | ✔ |
| grey level run length matrix | 16 | ✕ | ✔ | ✔ |
| grey level size zone matrix | 16 | ✕ | ✔ | ✔ |
| grey level distance zone matrix | 16 | ✔ | ✔ | ✔ |
| neighbourhood grey tone difference matrix | 5 | ✕ | ✔ | ✔ |
| neighbouring grey level dependence matrix | 17 | ✕ | ✔ | ✔ |
Though image processing parameters affect feature values, three other concepts influence feature values for many features: distance, feature aggregation and distance weighting. These are described below.
Grid distances¶
MPUJ
Grid distance is an important concept that is used by several feature families, particularly texture features. Grid distances can be measured in several ways. Let \(\mathbf{m}=\left(m_x,m_y,m_z\right)\) be the vector from a center voxel at \(\mathbf{k}=\left(k_x,k_y,k_z\right)\) to a neighbour voxel at \(\mathbf{k}+\mathbf{m}\). The following norms (distances) are used:
\(\ell_1\) norm or Manhattan norm (LIFZ):
\[\|\mathbf{m}\|_1 = |m_x| + |m_y| + |m_z|\]\(\ell_2\) norm or Euclidean norm (G9EV):
\[\|\mathbf{m}\|_2 = \sqrt{m_x^2 + m_y^2 + m_z^2}\]\(\ell_{\infty}\) norm or Chebyshev norm (PVMT):
\[\|\mathbf{m}\|_{\infty} = \text{max}(|m_x|,|m_y|,|m_z|)\]
An example of how the above norms differ in practice is shown in Fig. 8 .
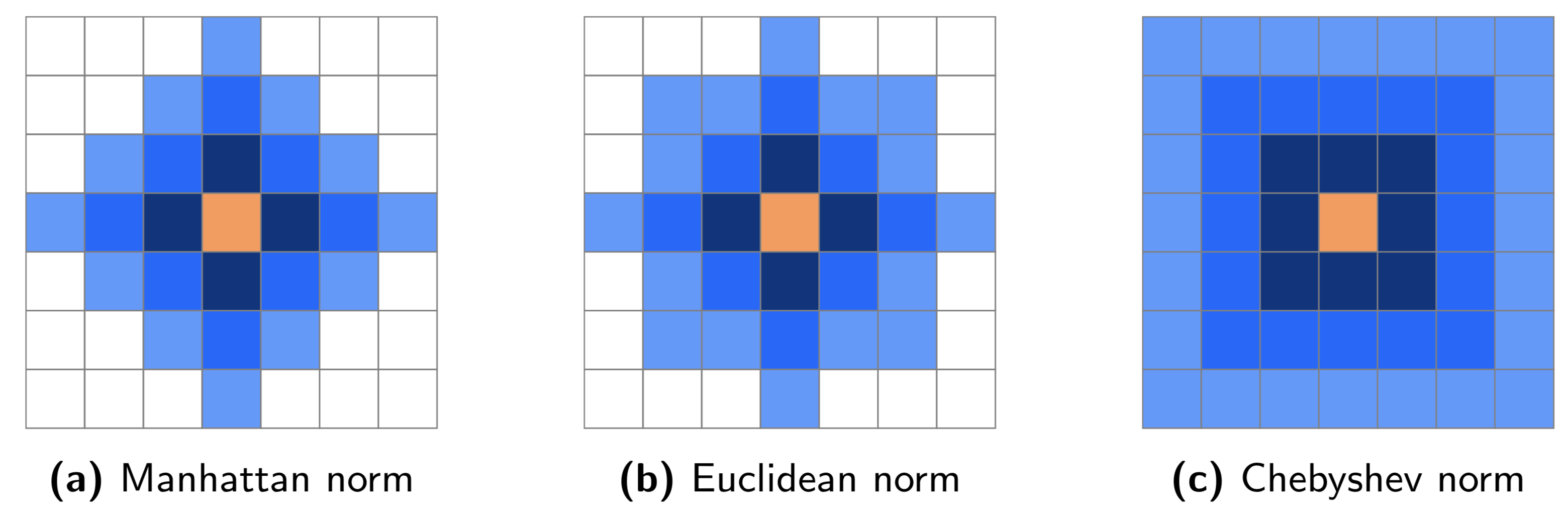
Fig. 8 Grid neighbourhoods for distances up to \(3\) according to Manhattan, Euclidean and Chebyshev norms. The orange pixel is considered the center pixel. Dark blue pixels have distance \(\delta=1\), blue pixels \(\delta\leq2\) and light blue pixels \(\delta\leq3\) for the corresponding norm.
Feature aggregation¶
5QB6
Features from some families may be calculated from, e.g. slices. As a consequence, multiple values for the same feature may be computed. These different values should be combined into a single value for many common purposes. This process is referred to as feature aggregation. Feature aggregation methods depend on the family, and are detailed in the family description.
Distance weighting¶
6CK8
Distance weighting is not a default operation for any of the texture families, but is implemented in software such as PyRadiomics [VanGriethuysen2017]. It may for example be used to put more emphasis on local intensities.
Morphological features¶
HCUG
Morphological features describe geometric aspects of a region of interest (ROI), such as area and volume. Morphological features are based on ROI voxel representations of the volume. Three voxel representations of the volume are conceivable:
- The volume is represented by a collection of voxels with each voxel taking up a certain volume (LQD8).
- The volume is represented by a voxel point set \(\mathbf{X}_{c}\) that consists of coordinates of the voxel centers (4KW8).
- The volume is represented by a surface mesh (WRJH).
We use the second representation when the inner structure of the volume is important, and the third representation when only the outer surface structure is important. The first representation is not used outside volume approximations because it does not handle partial volume effects at the ROI edge well, and also to avoid inconsistencies in feature values introduced by mixing representations in small voxel volumes.
Mesh-based representation¶
A mesh-based representation of the outer surface allows consistent evaluation of the surface volume and area independent of size. Voxel-based representations lead to partial volume effects and over-estimation of the surface area. The surface of the ROI volume is translated into a triangle mesh using a meshing algorithm. While multiple meshing algorithms exist, we suggest the use of the Marching Cubes algorithm [Lorensen1987][Lewiner2003] because of its widespread availability in different programming languages and reasonable approximation of the surface area and volume [Stelldinger2007]. In practice, mesh-based feature values depend upon the meshing algorithm and small differences may occur between implementations [Limkin2019jt].
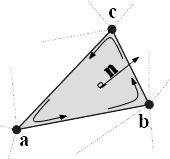
Fig. 9 Meshing algorithms draw faces and vertices to cover the ROI. One face, spanned by vertices \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{c}\), is highlighted. Moreover, the vertices define the three edges \(\mathbf{ab}=\mathbf{b}-\mathbf{a}\), \(\mathbf{bc}=\mathbf{c}-\mathbf{b}\) and \(\mathbf{ca}=\mathbf{a}-\mathbf{c}\). The face normal \(\mathbf{n}\) is determined using the right-hand rule, and calculated as \(\mathbf{n}=\left(\mathbf{ab} \times \mathbf{bc}\right) / \| \mathbf{ab} \times \mathbf{bc}\|\), i.e. the outer product of edge \(\mathbf{ab}\) with edge \(\mathbf{bc}\), normalised by its length.
Meshing algorithms use the ROI voxel point set \(\mathbf{X}_{c}\) to create a closed mesh. Dependent on the algorithm, a parameter is required to specify where the mesh should be drawn. A default level of 0.5 times the voxel spacing is used for marching cube algorithms. Other algorithms require a so-called isovalue, for which a value of 0.5 can be used since the ROI mask consists of \(0\) and \(1\) values, and we want to roughly draw the mesh half-way between voxel centers. Depending on implementation, algorithms may also require padding of the ROI mask with non-ROI (\(0\)) voxels to correctly estimate the mesh in places where ROI voxels would otherwise be located at the edge of the mask.
The closed mesh drawn by the meshing algorithm consists of \(N_{fc}\) triangle faces spanned by \(N_{vx}\) vertex points. An example triangle face is drawn in Fig. 9. The set of vertex points is then \(\mathbf{X}_{vx}\).
The calculation of the mesh volume requires that all faces have the same orientation of the face normal. Consistent orientation can be checked by the fact that in a regular, closed mesh, all edges are shared between exactly two faces. Given the edge spanned by vertices \(\mathbf{a}\) and \(\mathbf{b}\), the edge must be \(\mathbf{ab}=\mathbf{b}-\mathbf{a}\) for one face and \(\mathbf{ba}=\mathbf{a}-\mathbf{b}\) for the adjacent face. This ensures consistent application of the right-hand rule, and thus consistent orientation of the face normals. Algorithm implementations may return consistently orientated faces by default.
ROI morphological and intensity masks¶
The ROI consists of a morphological and an intensity mask. The morphological mask is used to calculate many of the morphological features and to generate the voxel point set \(\mathbf{X}_{c}\). Any holes within the morphological mask are understood to be the result of segmentation decisions, and thus to be intentional. The intensity mask is used to generate the voxel intensity set \(\mathbf{X}_{gl}\) with corresponding point set \(\mathbf{X}_{c,gl}\).
Aggregating features¶
By definition, morphological features are calculated in 3D (DHQ4), and not per slice.
Units of measurement¶
By definition, morphological features are computed using the unit of length as defined in the DICOM standard, i.e. millimeter for most medical imaging modalities.
If the unit of length is not defined by a standard, but is explicitly defined as meta data, this definition should be used. In this case, care should be taken that this definition is consistent across all data in the cohort.
If a feature value should be expressed as a different unit of length, e.g. cm instead of mm, such conversions should take place after computing the value using the standard units.
Volume (mesh)¶
RNU0
The mesh-based volume \(V\) is calculated from the ROI mesh as follows [Zhang2001]. A tetrahedron is formed by each face \(k\) and the origin. By placing the origin vertex of each tetrahedron at \((0,0,0)\), the signed volume of the tetrahedron is:
Here \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{c}\) are the vertex points of face \(k\). Depending on the orientation of the normal, the signed volume may be positive or negative. Hence, the orientation of face normals should be consistent, e.g. all normals must be either pointing outward or inward. The volume \(V\) is then calculated by summing over the face volumes, and taking the absolute value:
In positron emission tomography, the volume of the ROI commonly receives a name related to the radioactive tracer, e.g. metabolically active tumour volume (MATV) for 18F-FDG.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 556 | 4 | very strong |
| config. A | \(3.58 \times 10^{5}\) | \(5 \times 10^{3}\) | very strong |
| config. B | \(3.58 \times 10^{5}\) | \(5 \times 10^{3}\) | strong |
| config. C | \(3.67 \times 10^{5}\) | \(6 \times 10^{3}\) | strong |
| config. D | \(3.67 \times 10^{5}\) | \(6 \times 10^{3}\) | strong |
| config. E | \(3.67 \times 10^{5}\) | \(6 \times 10^{3}\) | strong |
Volume (voxel counting)¶
YEKZ
In clinical practice, volumes are commonly determined by counting voxels. For volumes consisting of a large number of voxels (1000s), the differences between voxel counting and mesh-based approaches are usually negligible. However for volumes with a low number of voxels (10s to 100s), voxel counting will overestimate volume compared to the mesh-based approach. It is therefore only used as a reference feature, and not in the calculation of other morphological features.
Voxel counting volume is defined as:
Here \(N_v\) is the number of voxels in the morphological mask of the ROI, and \(V_k\) the volume of voxel \(k\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 592 | 4 | very strong |
| config. A | \(3.59 \times 10^{5}\) | \(5 \times 10^{3}\) | strong |
| config. B | \(3.58 \times 10^{5}\) | \(5 \times 10^{3}\) | strong |
| config. C | \(3.68 \times 10^{5}\) | \(6 \times 10^{3}\) | strong |
| config. D | \(3.68 \times 10^{5}\) | \(6 \times 10^{3}\) | strong |
| config. E | \(3.68 \times 10^{5}\) | \(6 \times 10^{3}\) | strong |
Surface area (mesh)¶
C0JK
The surface area \(A\) is also calculated from the ROI mesh by summing over the triangular face surface areas [Aerts2014]. By definition, the area of face \(k\) is:
As in Fig. 9, edge \(\mathbf{ab}=\mathbf{b}-\mathbf{a}\) is the vector from vertex \(\mathbf{a}\) to vertex \(\mathbf{b}\), and edge \(\mathbf{ac}=\mathbf{c}-\mathbf{a}\) the vector from vertex \(\mathbf{a}\) to vertex \(\mathbf{c}\). The total surface area \(A\) is then:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 388 | 3 | very strong |
| config. A | \(3.57 \times 10^{4}\) | 300 | strong |
| config. B | \(3.37 \times 10^{4}\) | 300 | strong |
| config. C | \(3.43 \times 10^{4}\) | 400 | strong |
| config. D | \(3.43 \times 10^{4}\) | 400 | strong |
| config. E | \(3.43 \times 10^{4}\) | 400 | strong |
Surface to volume ratio¶
2PR5
The surface to volume ratio is given as [Aerts2014]:
Note that this feature is not dimensionless.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.698 | 0.004 | very strong |
| config. A | 0.0996 | 0.0005 | strong |
| config. B | 0.0944 | 0.0005 | strong |
| config. C | 0.0934 | 0.0007 | strong |
| config. D | 0.0934 | 0.0007 | strong |
| config. E | 0.0934 | 0.0007 | strong |
Compactness 1¶
SKGS
Several features (compactness 1 and 2, spherical disproportion, sphericity and asphericity) quantify the deviation of the ROI volume from a representative spheroid. All these definitions can be derived from one another. As a results these features are are highly correlated and may thus be redundant. Compactness 1 [Aerts2014] is a measure for how compact, or sphere-like the volume is. It is defined as:
Compactness 1 is sometimes [Aerts2014] defined using \(A^{2/3}\) instead of \(A^{3/2}\), but this does not lead to a dimensionless quantity.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.0411 | 0.0003 | strong |
| config. A | 0.03 | 0.0001 | strong |
| config. B | 0.0326 | 0.0001 | strong |
| config. C | — | — | moderate |
| config. D | 0.0326 | 0.0002 | strong |
| config. E | 0.0326 | 0.0002 | strong |
Compactness 2¶
BQWJ
Like Compactness 1, Compactness 2 [Aerts2014] quantifies how sphere-like the volume is:
By definition \(F_{\mathit{morph.comp.1}} = 1/6\pi \left(F_{\mathit{morph.comp.2}}\right)^{1/2}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.599 | 0.004 | strong |
| config. A | 0.319 | 0.001 | strong |
| config. B | 0.377 | 0.001 | strong |
| config. C | 0.378 | 0.004 | strong |
| config. D | 0.378 | 0.004 | strong |
| config. E | 0.378 | 0.004 | strong |
Spherical disproportion¶
KRCK
Spherical disproportion [Aerts2014] likewise describes how sphere-like the volume is:
By definition \(F_{\mathit{morph.sph.dispr}} = \left(F_{\mathit{morph.comp.2}}\right)^{-1/3}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1.19 | 0.01 | strong |
| config. A | 1.46 | 0.01 | strong |
| config. B | 1.38 | 0.01 | strong |
| config. C | 1.38 | 0.01 | strong |
| config. D | 1.38 | 0.01 | strong |
| config. E | 1.38 | 0.01 | strong |
Sphericity¶
QCFX
Sphericity [Aerts2014] is a further measure to describe how sphere-like the volume is:
By definition \(F_{\mathit{morph.sphericity}} = \left(F_{\mathit{morph.comp.2}}\right)^{1/3}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.843 | 0.005 | very strong |
| config. A | 0.683 | 0.001 | strong |
| config. B | 0.722 | 0.001 | strong |
| config. C | 0.723 | 0.003 | strong |
| config. D | 0.723 | 0.003 | strong |
| config. E | 0.723 | 0.003 | strong |
Asphericity¶
25C7
Asphericity [Apostolova2014] also describes how much the ROI deviates from a perfect sphere, with perfectly spherical volumes having an asphericity of 0. Asphericity is defined as:
By definition \(F_{\mathit{morph.asphericity}} = \left(F_{\mathit{morph.comp.2}}\right)^{-1/3}-1\)
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.186 | 0.001 | strong |
| config. A | 0.463 | 0.002 | strong |
| config. B | 0.385 | 0.001 | moderate |
| config. C | 0.383 | 0.004 | strong |
| config. D | 0.383 | 0.004 | strong |
| config. E | 0.383 | 0.004 | strong |
Centre of mass shift¶
KLMA
The distance between the ROI volume centroid and the intensity-weighted ROI volume is an abstraction of the spatial distribution of low/high intensity regions within the ROI. Let \(N_{v,m}\) be the number of voxels in the morphological mask. The ROI volume centre of mass is calculated from the morphological voxel point set \(\mathbf{X}_{c}\) as follows:
The intensity-weighted ROI volume is based on the intensity mask. The position of each voxel centre in the intensity mask voxel set \(\mathbf{X}_{c,gl}\) is weighted by its corresponding intensity \(\mathbf{X}_{gl}\). Therefore, with \(N_{v,gl}\) the number of voxels in the intensity mask:
The distance between the two centres of mass is then:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.672 | 0.004 | very strong |
| config. A | 52.9 | 28.7 | strong |
| config. B | 63.1 | 29.6 | strong |
| config. C | 45.6 | 2.8 | strong |
| config. D | 64.9 | 2.8 | strong |
| config. E | 68.5 | 2.1 | moderate |
Maximum 3D diameter¶
L0JK
The maximum 3D diameter [Aerts2014] is the distance between the two most distant vertices in the ROI mesh vertex set \(\mathbf{X}_{vx}\):
A practical way of determining the maximum 3D diameter is to first construct the convex hull of the ROI mesh. The convex hull vertex set \(\mathbf{X}_{vx,convex}\) is guaranteed to contain the two most distant vertices of \(\mathbf{X}_{vx}\). This significantly reduces the computational cost of calculating distances between all vertices. Despite the remaining \(O(n^2)\) cost of calculating distances between different vertices, \(\mathbf{X}_{vx,convex}\) is usually considerably smaller in size than \(\mathbf{X}_{vx}\). Moreover, the convex hull is later used for the calculation of other morphological features (Volume density (convex hull) - Area density (convex hull)).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 13.1 | 0.1 | strong |
| config. A | 125 | 1 | strong |
| config. B | 125 | 1 | strong |
| config. C | 125 | 1 | strong |
| config. D | 125 | 1 | strong |
| config. E | 125 | 1 | strong |
Major axis length¶
TDIC
Principal component analysis (PCA) can be used to determine the main orientation of the ROI [Solomon2011]. On a three dimensional object, PCA yields three orthogonal eigenvectors \(\left\lbrace e_1,e_2,e_3\right\rbrace\) and three eigenvalues \(\left( \lambda_1, \lambda_2, \lambda_3\right)\). These eigenvalues and eigenvectors geometrically describe a triaxial ellipsoid. The three eigenvectors determine the orientation of the ellipsoid, whereas the eigenvalues provide a measure of how far the ellipsoid extends along each eigenvector. Several features make use of principal component analysis, namely major, minor and least axis length, elongation, flatness, and approximate enclosing ellipsoid volume and area density.
The eigenvalues can be ordered so that \(\lambda_{\mathit{major}} \geq \lambda_{\mathit{minor}}\geq \lambda_{\mathit{least}}\) correspond to the major, minor and least axes of the ellipsoid respectively. The semi-axes lengths \(a\), \(b\) and \(c\) for the major, minor and least axes are then \(2\sqrt{\lambda_{\mathit{major}}}\), \(2\sqrt{\lambda_{\mathit{minor}}}\) and \(2\sqrt{\lambda_{\mathit{least}}}\) respectively. The major axis length is twice the semi-axis length \(a\), determined using the largest eigenvalue obtained by PCA on the point set of voxel centers \(\mathbf{X}_{c}\) [Heiberger2015]:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 11.4 | 0.1 | very strong |
| config. A | 92.7 | 0.4 | very strong |
| config. B | 92.6 | 0.4 | strong |
| config. C | 93.3 | 0.5 | strong |
| config. D | 93.3 | 0.5 | strong |
| config. E | 93.3 | 0.5 | strong |
Minor axis length¶
P9VJ
The minor axis length of the ROI provides a measure of how far the volume extends along the second largest axis. The minor axis length is twice the semi-axis length \(b\), determined using the second largest eigenvalue obtained by PCA, as described in Section Major axis length.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 9.31 | 0.06 | very strong |
| config. A | 81.5 | 0.4 | very strong |
| config. B | 81.3 | 0.4 | strong |
| config. C | 82 | 0.5 | strong |
| config. D | 82 | 0.5 | strong |
| config. E | 82 | 0.5 | strong |
Least axis length¶
7J51
The least axis is the axis along which the object is least extended. The least axis length is twice the semi-axis length \(c\), determined using the smallest eigenvalue obtained by PCA, as described in Section Major axis length.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 8.54 | 0.05 | very strong |
| config. A | 70.1 | 0.3 | strong |
| config. B | 70.2 | 0.3 | strong |
| config. C | 70.9 | 0.4 | strong |
| config. D | 70.9 | 0.4 | strong |
| config. E | 70.9 | 0.4 | strong |
Elongation¶
Q3CK
The ratio of the major and minor principal axis lengths could be viewed as the extent to which a volume is longer than it is wide, i.e. is eccentric. For computational reasons, we express elongation as an inverse ratio. 1 is thus completely non-elongated, e.g. a sphere, and smaller values express greater elongation of the ROI volume.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.816 | 0.005 | very strong |
| config. A | 0.879 | 0.001 | strong |
| config. B | 0.878 | 0.001 | strong |
| config. C | 0.879 | 0.001 | strong |
| config. D | 0.879 | 0.001 | strong |
| config. E | 0.879 | 0.001 | strong |
Flatness¶
N17B
The ratio of the major and least axis lengths could be viewed as the extent to which a volume is flat relative to its length. For computational reasons, we express flatness as an inverse ratio. 1 is thus completely non-flat, e.g. a sphere, and smaller values express objects which are increasingly flatter.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.749 | 0.005 | very strong |
| config. A | 0.756 | 0.001 | strong |
| config. B | 0.758 | 0.001 | strong |
| config. C | 0.76 | 0.001 | strong |
| config. D | 0.76 | 0.001 | strong |
| config. E | 0.76 | 0.001 | strong |
Volume density (axis-aligned bounding box)¶
PBX1
Volume density is the fraction of the ROI volume and a comparison volume. Here the comparison volume is that of the axis-aligned bounding box (AABB) of the ROI mesh vertex set \(\mathbf{X}_{vx}\) or the ROI mesh convex hull vertex set \(\mathbf{X}_{vx,convex}\). Both vertex sets generate an identical bounding box, which is the smallest box enclosing the vertex set, and aligned with the axes of the reference frame.
This feature is also called extent [ElNaqa2009][Solomon2011].
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.869 | 0.005 | strong |
| config. A | 0.486 | 0.003 | strong |
| config. B | 0.477 | 0.003 | strong |
| config. C | 0.478 | 0.003 | strong |
| config. D | 0.478 | 0.003 | strong |
| config. E | 0.478 | 0.003 | strong |
Area density (axis-aligned bounding box)¶
R59B
Conceptually similar to the volume density (AABB) feature, area density considers the ratio of the ROI surface area and the surface area \(A_{aabb}\) of the axis-aligned bounding box enclosing the ROI mesh vertex set \(\mathbf{X}_{vx}\) [VanDijk2016]. The bounding box is identical to the one used for computing the volume density (AABB) feature. Thus:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.866 | 0.005 | strong |
| config. A | 0.725 | 0.003 | strong |
| config. B | 0.678 | 0.003 | strong |
| config. C | 0.678 | 0.003 | strong |
| config. D | 0.678 | 0.003 | strong |
| config. E | 0.678 | 0.003 | strong |
Volume density (oriented minimum bounding box)¶
ZH1A
Note: This feature currently has no reference values and should not be used.
The volume of an axis-aligned bounding box is generally not the smallest obtainable volume enclosing the ROI. By orienting the box along a different set of axes, a smaller enclosing volume may be attainable. The oriented minimum bounding box (OMBB) of the ROI mesh vertex set \(\mathbf{X}_{vx}\) or \(\mathbf{X}_{vx,convex}\) encloses the vertex set and has the smallest possible volume. A 3D rotating callipers technique was devised by [ORourke1985] to derive the oriented minimum bounding box. Due to computational complexity of this technique, the oriented minimum bounding box is commonly approximated at lower complexity, see e.g. [Barequet2001] and [Chan2001]. Thus:
Here \(V_{ombb}\) is the volume of the oriented minimum bounding box.
Area density (oriented minimum bounding box)¶
IQYR
Note: This feature currently has no reference values and should not be used.
The area density (OMBB) is estimated as:
Here \(A_{ombb}\) is the surface area of the same bounding box as calculated for the volume density (OMBB) feature.
Volume density (approximate enclosing ellipsoid)¶
6BDE
The eigenvectors and eigenvalues from PCA of the ROI voxel center point set \(\mathbf{X}_{c}\) can be used to describe an ellipsoid approximating the point cloud [Mazurowski2016], i.e. the approximate enclosing ellipsoid (AEE). The volume of this ellipsoid is \(V_{\mathit{aee}}=4 \pi\,a\,b\,c /3\), with \(a\), \(b\), and \(c\) being the lengths of the ellipsoid’s semi-principal axes, see Section Major axis length. The volume density (AEE) is then:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1.17 | 0.01 | moderate |
| config. A | 1.29 | 0.01 | strong |
| config. B | 1.29 | 0.01 | strong |
| config. C | 1.29 | 0.01 | moderate |
| config. D | 1.29 | 0.01 | moderate |
| config. E | 1.29 | 0.01 | strong |
Area density (approximate enclosing ellipsoid)¶
RDD2
The surface area of an ellipsoid can generally not be evaluated in an elementary form. However, it is possible to approximate the surface using an infinite series. We use the same semi-principal axes as for the volume density (AEE) feature and define:
Here \(\alpha=\sqrt{1-b^2/a^2}\) and \(\beta=\sqrt{1-c^2/a^2}\) are eccentricities of the ellipsoid and \(P_{\nu}\) is the Legendre polynomial function for degree \(\nu\). The Legendre polynomial series, though infinite, converges, and approximation may be stopped early when the incremental gains in precision become limited. By default, we stop the series after \(\nu=20\).
The area density (AEE) is then approximated as:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1.36 | 0.01 | moderate |
| config. A | 1.71 | 0.01 | moderate |
| config. B | 1.62 | 0.01 | moderate |
| config. C | 1.62 | 0.01 | moderate |
| config. D | 1.62 | 0.01 | moderate |
| config. E | 1.62 | 0.01 | strong |
Volume density (minimum volume enclosing ellipsoid)¶
SWZ1
Note: This feature currently has no reference values and should not be used.
The minimum volume enclosing ellipsoid (MVEE), unlike the approximate enclosing ellipsoid, is the smallest ellipsoid that encloses the ROI. Direct computation of the MVEE is usually unfeasible, and is therefore approximated. Various approximation algorithms have been described, e.g. [Todd2007][Ahipasaoglu2015], which are usually elaborations on Khachiyan’s barycentric coordinate descent method [Khachiyan1996].
The MVEE encloses the ROI mesh vertex set \(\mathbf{X}_{vx}\), and by definition \(\mathbf{X}_{vx,convex}\) as well. Use of the convex mesh set \(\mathbf{X}_{vx,convex}\) is recommended due to its sparsity compared to the full vertex set. The volume of the MVEE is defined by its semi-axes lengths \(V_{\mathit{mvee}}=4 \pi\,a\,b\,c /3\). Then:
For Khachiyan’s barycentric coordinate descent-based methods we use a default tolerance \(\tau=0.001\) as stopping criterion.
Area density (minimum volume enclosing ellipsoid)¶
BRI8
Note: This feature currently has no reference values and should not be used.
The surface area of an ellipsoid does not have a general elementary form, but should be approximated as noted in Section Area density (approximate enclosing ellipsoid). Let the approximated surface area of the MVEE be \(A_{\mathit{mvee}}\). Then:
Volume density (convex hull)¶
R3ER
The convex hull encloses ROI mesh vertex set \(\mathbf{X}_{vx}\) and consists of the vertex set \(\mathbf{X}_{vx,convex}\) and corresponding faces, see section Maximum 3D diameter. The volume of the ROI mesh convex hull set \(V_{convex}\) is computed in the same way as that of the volume (mesh) feature (Volume (mesh)). The volume density can then be calculated as follows:
This feature is also called solidity [ElNaqa2009][Solomon2011].
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.961 | 0.006 | strong |
| config. A | 0.827 | 0.001 | moderate |
| config. B | 0.829 | 0.001 | moderate |
| config. C | 0.834 | 0.002 | moderate |
| config. D | 0.834 | 0.002 | moderate |
| config. E | 0.834 | 0.002 | moderate |
Area density (convex hull)¶
7T7F
The area of the convex hull \(A_{convex}\) is the sum of the areas of the faces of the convex hull, and is computed in the same way as the surface area (mesh) feature (Surface area (mesh) section). The convex hull is identical to the one used in the volume density (convex hull) feature. Then:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1.03 | 0.01 | strong |
| config. A | 1.18 | 0.01 | moderate |
| config. B | 1.12 | 0.01 | moderate |
| config. C | 1.13 | 0.01 | moderate |
| config. D | 1.13 | 0.01 | moderate |
| config. E | 1.13 | 0.01 | moderate |
Integrated intensity¶
99N0
Integrated intensity is the average intensity in the ROI, multiplied by the volume. In the context of 18F-FDG-PET, this feature is often called total lesion glycolysis [Vaidya2012]. Thus:
\(N_{v,gl}\) is the number of voxels in the ROI intensity mask.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | \(1.2 \times 10^{3}\) | 10 | moderate |
| config. A | \(4.81 \times 10^{6}\) | \(3.2 \times 10^{5}\) | strong |
| config. B | \(4.12 \times 10^{6}\) | \(3.2 \times 10^{5}\) | strong |
| config. C | \(-1.8 \times 10^{7}\) | \(1.4 \times 10^{6}\) | strong |
| config. D | \(-8.64 \times 10^{6}\) | \(1.56 \times 10^{6}\) | strong |
| config. E | \(-8.31 \times 10^{6}\) | \(1.6 \times 10^{6}\) | strong |
Moran’s I index¶
N365
Moran’s I index is an indicator of spatial autocorrelation [Moran1950][Dale2002]. It is defined as:
As before \(N_{v,gl}\) is the number of voxels in the ROI intensity mask, \(\mu\) is the mean of \(\mathbf{X}_{gl}\) and \(w_{k_{1}k_{2}}\) is a weight factor, equal to the inverse Euclidean distance between voxels \(k_{1}\) and \(k_{2}\) of the point set \(\mathbf{X}_{c,gl}\) of the ROI intensity mask [DaSilva2008]. Values of Moran’s I close to 1.0, 0.0 and -1.0 indicate high spatial autocorrelation, no spatial autocorrelation and high spatial anti-autocorrelation, respectively.
Note that for an ROI containing many voxels, calculating Moran’s I index may be computationally expensive due to \(O(n^2)\) behaviour. Approximation by repeated subsampling of the ROI may be required to make the calculation tractable, at the cost of accuracy.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.0397 | 0.0003 | strong |
| config. A | 0.0322 | 0.0002 | moderate |
| config. B | 0.0329 | 0.0001 | moderate |
| config. C | 0.0824 | 0.0003 | moderate |
| config. D | 0.0622 | 0.0013 | moderate |
| config. E | 0.0596 | 0.0014 | moderate |
Geary’s C measure¶
NPT7
Geary’s C measure assesses spatial autocorrelation, similar to Moran’s I index [Geary1954][Dale2002]. In contrast to Moran’s I index, Geary’s C measure directly assesses intensity differences between voxels and is more sensitive to local spatial autocorrelation. This measure is defined as:
As with Moran’s I, \(N_{v,gl}\) is the number of voxels in the ROI intensity mask, \(\mu\) is the mean of \(\mathbf{X}_{gl}\) and \(w_{k_{1}k_{2}}\) is a weight factor, equal to the inverse Euclidean distance between voxels \(k_{1}\) and \(k_{2}\) of the ROI voxel point set \(\mathbf{X}_{c,gl}\) [DaSilva2008].
Just as Moran’s I, Geary’s C measure exhibits \(O(n^2)\) behaviour and an approximation scheme may be required to make calculation feasible for large ROIs.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.974 | 0.006 | strong |
| config. A | 0.863 | 0.001 | moderate |
| config. B | 0.862 | 0.001 | moderate |
| config. C | 0.846 | 0.001 | moderate |
| config. D | 0.851 | 0.001 | moderate |
| config. E | 0.853 | 0.001 | moderate |
Local intensity features¶
9ST6
Voxel intensities within a defined neighbourhood around a center voxel are used to compute local intensity features. Unlike many other feature sets, local features do not draw solely on intensities within the ROI. While only voxels within the ROI intensity map can be used as a center voxel, the local neighbourhood draws upon all voxels regardless of being in an ROI.
Aggregating features¶
By definition, local intensity features are calculated in 3D (DHQ4), and not per slice.
Local intensity peak¶
VJGA
The local intensity peak was originally devised for reducing variance in determining standardised uptake values [Wahl2009]. It is defined as the mean intensity in a 1 cm3 spherical volume (in world coordinates), which is centered on the voxel with the maximum intensity level in the ROI intensity mask [Frings2014].
To calculate \(F_{\mathit{loc.peak.local}}\), we first select all the voxels with centers within a radius \(r=\left(\frac{3}{4 \pi}\right)^{1/3} \approx 0.62\) cm of the center of the maximum intensity voxel. Subsequently, the mean intensity of the selected voxels, including the center voxel, are calculated.
In case the maximum intensity is found in multiple voxels within the ROI, local intensity peak is calculated for each of these voxels, and the highest local intensity peak is chosen.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 2.6 | — | strong |
| config. A | \(-\)277 | 10 | moderate |
| config. B | 178 | 10 | moderate |
| config. C | 169 | 10 | moderate |
| config. D | 201 | 10 | strong |
| config. E | 181 | 13 | moderate |
Global intensity peak¶
0F91
The global intensity peak feature \(F_{\mathit{loc.peak.global}}\) is similar to the local intensity peak [Frings2014]. However, instead of calculating the mean intensity for the voxel(s) with the maximum intensity, the mean intensity is calculated within a 1 cm3 neighbourhood for every voxel in the ROI intensity mask. The highest intensity peak value is then selected.
Calculation of the global intensity peak feature may be accelerated by construction and application of an appropriate spatial spherical mean convolution filter, due to the convolution theorem. In this case one would first construct an empty 3D filter that will fit a 1 cm3 sphere. Within this context, the filter voxels may be represented by a point set, akin to \(\mathbf{X}_{c}\) in Morphological features. Euclidean distances in world spacing between the central voxel of the filter and every remaining voxel are computed. If this distance lies within radius \(r=\left(\frac{3}{4 \pi}\right)^{1/3} \approx 0.62\) the corresponding voxel receives a label \(1\), and \(0\) otherwise. Subsequent summation of the voxel labels yields \(N_s\), the number of voxels within the 1 cm3 sphere. The filter then becomes a spherical mean filter by dividing the labels by \(N_s\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 3.1 | — | strong |
| config. A | 189 | 5 | moderate |
| config. B | 178 | 5 | moderate |
| config. C | 180 | 5 | moderate |
| config. D | 201 | 5 | moderate |
| config. E | 181 | 5 | moderate |
Intensity-based statistical features¶
UHIW
The intensity-based statistical features describe how intensities within the region of interest (ROI) are distributed. The features in this set do not require discretisation, and may be used to describe a continuous intensity distribution. Intensity-based statistical features are not meaningful if the intensity scale is arbitrary.
The set of intensities of the \(N_v\) voxels included in the ROI intensity mask is denoted as \(\mathbf{X}_{gl}=\left\lbrace X_{gl,1},X_{gl,2},\ldots,X_{gl,N_v}\right\rbrace\).
Aggregating features¶
We recommend calculating intensity-based statistical features using the 3D volume (DHQ4). An approach that computes intensity-based statistical features per slice and subsequently averages them (3IDG) is not recommended.
Mean intensity¶
Q4LE
The mean intensity of \(\mathbf{X}_{gl}\) is calculated as:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 2.15 | — | very strong |
| config. A | 13.4 | 1.1 | very strong |
| config. B | 11.5 | 1.1 | strong |
| config. C | \(-\)49 | 2.9 | very strong |
| config. D | \(-\)23.5 | 3.9 | strong |
| config. E | \(-\)22.6 | 4.1 | strong |
Intensity variance¶
ECT3
The intensity variance of \(\mathbf{X}_{gl}\) is defined as:
Note that we do not apply a bias correction when computing the variance.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 3.05 | — | very strong |
| config. A | \(1.42 \times 10^{4}\) | 400 | very strong |
| config. B | \(1.44 \times 10^{4}\) | 400 | very strong |
| config. C | \(5.06 \times 10^{4}\) | \(1.4 \times 10^{3}\) | strong |
| config. D | \(3.28 \times 10^{4}\) | \(2.1 \times 10^{3}\) | strong |
| config. E | \(3.51 \times 10^{4}\) | \(2.2 \times 10^{3}\) | strong |
Intensity skewness¶
KE2A
The skewness of the intensity distribution of \(\mathbf{X}_{gl}\) is defined as:
Here \(\mu=F_{\mathit{stat.mean}}\). If the intensity variance \(F_{\mathit{stat.var}} = 0\), \(F_{\mathit{stat.skew}}=0\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1.08 | — | very strong |
| config. A | \(-\)2.47 | 0.05 | very strong |
| config. B | \(-\)2.49 | 0.05 | very strong |
| config. C | \(-\)2.14 | 0.05 | very strong |
| config. D | \(-\)2.28 | 0.06 | strong |
| config. E | \(-\)2.3 | 0.07 | strong |
(Excess) intensity kurtosis¶
IPH6
Kurtosis, or technically excess kurtosis, is a measure of peakedness in the intensity distribution \(\mathbf{X}_{gl}\):
Here \(\mu=F_{\mathit{stat.mean}}\). Note that kurtosis is corrected by a Fisher correction of -3 to center it on 0 for normal distributions. If the intensity variance \(F_{\mathit{stat.var}} = 0\), \(F_{\mathit{stat.kurt}}=0\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | \(-\)0.355 | — | very strong |
| config. A | 5.96 | 0.24 | very strong |
| config. B | 5.93 | 0.24 | very strong |
| config. C | 3.53 | 0.23 | very strong |
| config. D | 4.35 | 0.32 | strong |
| config. E | 4.44 | 0.33 | strong |
Median intensity¶
Y12H
The median intensity \(F_{\mathit{stat.median}}\) is the sample median of \(\mathbf{X}_{gl}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1 | — | very strong |
| config. A | 46 | 0.3 | very strong |
| config. B | 45 | 0.3 | strong |
| config. C | 40 | 0.4 | strong |
| config. D | 42 | 0.4 | strong |
| config. E | 43 | 0.5 | strong |
Minimum intensity¶
1GSF
The minimum intensity is equal to the lowest intensity present in \(\mathbf{X}_{gl}\), i.e:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1 | — | very strong |
| config. A | \(-\)500 | — | very strong |
| config. B | \(-\)500 | — | very strong |
| config. C | \(-\)939 | 4 | strong |
| config. D | \(-\)724 | 12 | strong |
| config. E | \(-\)743 | 13 | strong |
10th intensity percentile¶
QG58
\(P_{10}\) is the 10th percentile of \(\mathbf{X}_{gl}\). \(P_{10}\) is a more robust alternative to the minimum intensity.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1 | — | very strong |
| config. A | \(-\)129 | 8 | strong |
| config. B | \(-\)136 | 8 | strong |
| config. C | \(-\)424 | 14 | very strong |
| config. D | \(-\)304 | 20 | strong |
| config. E | \(-\)310 | 21 | strong |
90th intensity percentile¶
8DWT
\(P_{90}\) is the 90th percentile of \(\mathbf{X}_{gl}\). \(P_{90}\) is a more robust alternative to the maximum intensity.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 4 | — | very strong |
| config. A | 95 | — | strong |
| config. B | 91 | — | strong |
| config. C | 86 | 0.1 | strong |
| config. D | 86 | 0.1 | strong |
| config. E | 93 | 0.2 | strong |
Note that the 90:sup:`th` intensity percentile obtained for the digital phantom may differ from the above reference value depending on the software implementation used to compute it. For example, some implementations were found to produce a value of 4.2 instead of 4.
Maximum intensity¶
84IY
The maximum intensity is equal to the highest intensity present in \(\mathbf{X}_{gl}\), i.e:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 6 | — | very strong |
| config. A | 377 | 9 | very strong |
| config. B | 391 | 9 | strong |
| config. C | 393 | 10 | very strong |
| config. D | 521 | 22 | strong |
| config. E | 345 | 9 | strong |
Intensity interquartile range¶
SALO
The interquartile range (IQR) of \(\mathbf{X}_{gl}\) is defined as:
\(P_{25}\) and \(P_{75}\) are the 25th and 75th percentiles of \(\mathbf{X}_{gl}\), respectively.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 3 | — | very strong |
| config. A | 56 | 0.5 | very strong |
| config. B | 52 | 0.5 | strong |
| config. C | 67 | 4.9 | very strong |
| config. D | 57 | 4.1 | strong |
| config. E | 62 | 3.5 | strong |
Intensity range¶
2OJQ
The intensity range is defined as:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 5 | — | very strong |
| config. A | 877 | 9 | very strong |
| config. B | 891 | 9 | strong |
| config. C | \(1.33 \times 10^{3}\) | 20 | strong |
| config. D | \(1.24 \times 10^{3}\) | 40 | strong |
| config. E | \(1.09 \times 10^{3}\) | 30 | strong |
Intensity-based mean absolute deviation¶
4FUA
Mean absolute deviation is a measure of dispersion from the mean of \(\mathbf{X}_{gl}\):
Here \(\mu=F_{\mathit{stat.mean}}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1.55 | — | very strong |
| config. A | 73.6 | 1.4 | very strong |
| config. B | 74.4 | 1.4 | strong |
| config. C | 158 | 4 | very strong |
| config. D | 123 | 6 | strong |
| config. E | 125 | 6 | strong |
Intensity-based robust mean absolute deviation¶
1128
The intensity-based mean absolute deviation feature may be influenced by outliers. To increase robustness, the set of intensities can be restricted to those which lie closer to the center of the distribution. Let
Then \(\mathbf{X}_{gl,10-90}\) is the set of \(N_{v,10-90}\leq N_v\) voxels in \(\mathbf{X}_{gl}\) whose intensities fall in the interval bounded by the 10th and 90th percentiles of \(\mathbf{X}_{gl}\). The robust mean absolute deviation is then:
\(\overline{X}_{gl,10-90}\) denotes the sample mean of \(\mathbf{X_{gl,10-90}}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1.11 | — | very strong |
| config. A | 27.7 | 0.8 | very strong |
| config. B | 27.3 | 0.8 | strong |
| config. C | 66.8 | 3.5 | very strong |
| config. D | 46.8 | 3.6 | strong |
| config. E | 46.5 | 3.7 | strong |
Intensity-based median absolute deviation¶
N72L
Median absolute deviation is similar in concept to the intensity-based mean absolute deviation, but measures dispersion from the median intensity instead of the mean intensity. Thus:
Here, median \(M = F_{\mathit{stat.median}}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1.15 | — | very strong |
| config. A | 64.3 | 1 | strong |
| config. B | 63.8 | 1 | strong |
| config. C | 119 | 4 | strong |
| config. D | 94.7 | 3.8 | strong |
| config. E | 97.9 | 3.9 | strong |
Intensity-based coefficient of variation¶
7TET
The coefficient of variation measures the dispersion of \(\mathbf{X}_{gl}\). It is defined as:
Here \(\sigma={F_{\mathit{stat.var}}}^{1/2}\) and \(\mu=F_{\mathit{stat.mean}}\) are the standard deviation and mean of the intensity distribution, respectively.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.812 | — | very strong |
| config. A | 8.9 | 4.98 | strong |
| config. B | 10.4 | 5.2 | strong |
| config. C | \(-\)4.59 | 0.29 | strong |
| config. D | \(-\)7.7 | 1.01 | strong |
| config. E | \(-\)8.28 | 0.95 | strong |
Intensity-based quartile coefficient of dispersion¶
9S40
The quartile coefficient of dispersion is a more robust alternative to the intensity-based coefficient of variance. It is defined as:
\(P_{25}\) and \(P_{75}\) are the 25th and 75th percentile of \(\mathbf{X}_{gl}\), respectively.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.6 | — | very strong |
| config. A | 0.636 | 0.008 | strong |
| config. B | 0.591 | 0.008 | strong |
| config. C | 1.03 | 0.4 | strong |
| config. D | 0.74 | 0.011 | strong |
| config. E | 0.795 | 0.337 | strong |
Intensity-based energy¶
N8CA
The energy [Aerts2014] of \(\mathbf{X}_{gl}\) is defined as:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 567 | — | very strong |
| config. A | \(1.65 \times 10^{9}\) | \(2 \times 10^{7}\) | very strong |
| config. B | \(3.98 \times 10^{8}\) | \(1.1 \times 10^{7}\) | strong |
| config. C | \(2.44 \times 10^{9}\) | \(1.2 \times 10^{8}\) | strong |
| config. D | \(1.48 \times 10^{9}\) | \(1.4 \times 10^{8}\) | strong |
| config. E | \(1.58 \times 10^{9}\) | \(1.4 \times 10^{8}\) | strong |
Root mean square intensity¶
5ZWQ
The root mean square intensity feature [Aerts2014], which is also called the quadratic mean, of \(\mathbf{X}_{gl}\) is defined as:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 2.77 | — | very strong |
| config. A | 120 | 2 | very strong |
| config. B | 121 | 2 | strong |
| config. C | 230 | 4 | strong |
| config. D | 183 | 7 | strong |
| config. E | 189 | 7 | strong |
Intensity histogram features¶
ZVCW
An intensity histogram is generated by discretising the original intensity distribution \(\mathbf{X}_{gl}\) into intensity bins. Approaches to discretisation are described in Section Intensity discretisation.
Let \(\mathbf{X}_{d}=\left\lbrace X_{d,1},X_{d,2},\ldots,X_{d,N_v}\right\rbrace\) be the set of \(N_g\) discretised intensities of the \(N_v\) voxels in the ROI intensity mask. Let \(\mathbf{H}=\left\lbrace n_1, n_2,\ldots, n_{N_g}\right\rbrace\) be the histogram with frequency count \(n_i\) of each discretised intensity \(i\) in \(\mathbf{X}_{d}\). The occurrence probability \(p_i\) for each discretised intensity \(i\) is then approximated as \(p_i=n_i/N_v\).
Aggregating features¶
We recommend calculating intensity histogram features using the 3D volume (DHQ4). An approach that computes features per slice and subsequently averages (3IDG) is not recommended.
Mean discretised intensity¶
X6K6
The mean [Aerts2014] of \(\mathbf{X}_{d}\) is calculated as:
An equivalent definition is:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 2.15 | — | very strong |
| config. A | 21.1 | 0.1 | strong |
| config. B | 18.9 | 0.3 | strong |
| config. C | 38.6 | 0.2 | strong |
| config. D | 18.5 | 0.5 | strong |
| config. E | 21.7 | 0.3 | strong |
Discretised intensity variance¶
CH89
The variance [Aerts2014] of \(\mathbf{X}_{d}\) is defined as:
Here \(\mu=F_{\mathit{ih.mean}}\). This definition is equivalent to:
Note that no bias-correction is applied when computing the variance.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 3.05 | — | strong |
| config. A | 22.8 | 0.6 | strong |
| config. B | 18.7 | 0.2 | strong |
| config. C | 81.1 | 2.1 | strong |
| config. D | 21.7 | 0.4 | strong |
| config. E | 30.4 | 0.8 | strong |
Discretised intensity skewness¶
88K1
The skewness [Aerts2014] of \(\mathbf{X}_{d}\) is defined as:
Here \(\mu=F_{\mathit{ih.mean}}\). This definition is equivalent to:
If the discretised intensity variance \(F_{\mathit{ih.var}} = 0\), \(F_{\mathit{ih.skew}}=0\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1.08 | — | very strong |
| config. A | \(-\)2.46 | 0.05 | strong |
| config. B | \(-\)2.47 | 0.05 | strong |
| config. C | \(-\)2.14 | 0.05 | strong |
| config. D | \(-\)2.27 | 0.06 | strong |
| config. E | \(-\)2.29 | 0.07 | strong |
(Excess) discretised intensity kurtosis¶
C3I7
Kurtosis [Aerts2014], or technically excess kurtosis, measures the peakedness of the \(\mathbf{X}_{d}\) distribution:
Here \(\mu=F_{\mathit{ih.mean}}\). An alternative, but equivalent, definition is:
Note that kurtosis is corrected by a Fisher correction of -3 to center kurtosis on 0 for normal distributions. If the discretised intensity variance \(F_{\mathit{ih.var}} = 0\), \(F_{\mathit{ih.kurt}}=0\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | \(-\)0.355 | — | very strong |
| config. A | 5.9 | 0.24 | strong |
| config. B | 5.84 | 0.24 | strong |
| config. C | 3.52 | 0.23 | strong |
| config. D | 4.31 | 0.32 | strong |
| config. E | 4.4 | 0.33 | strong |
Median discretised intensity¶
WIFQ
The median \(F_{\mathit{ih.median}}\) is the sample median of \(\mathbf{X}_{d}\) [Aerts2014].
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1 | — | very strong |
| config. A | 22 | — | strong |
| config. B | 20 | 0.3 | strong |
| config. C | 42 | — | strong |
| config. D | 20 | 0.5 | strong |
| config. E | 24 | 0.2 | strong |
Minimum discretised intensity¶
1PR8
The minimum discretised intensity [Aerts2014] is equal to the lowest discretised intensity present in \(\mathbf{X}_{d}\), i.e.:
For fixed bin number discretisation \(F_{\mathit{ih.min}}=1\) by definition, but \(F_{\mathit{ih.min}}>1\) is possible for fixed bin size discretisation.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1 | — | very strong |
| config. A | 1 | — | strong |
| config. B | 1 | — | strong |
| config. C | 3 | 0.16 | strong |
| config. D | 1 | — | strong |
| config. E | 1 | — | strong |
10th discretised intensity percentile¶
1PR8
\(P_{10}\) is the 10th percentile of \(\mathbf{X}_{d}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1 | — | very strong |
| config. A | 15 | 0.4 | strong |
| config. B | 14 | 0.5 | strong |
| config. C | 24 | 0.7 | strong |
| config. D | 11 | 0.7 | strong |
| config. E | 13 | 0.7 | strong |
90th discretised intensity percentile¶
GPMT
\(P_{90}\) is the 90th percentile of \(\mathbf{X}_{d}\) and is defined as \(F_{\mathit{ih.P90}}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 4 | — | strong |
| config. A | 24 | — | strong |
| config. B | 22 | 0.3 | strong |
| config. C | 44 | — | strong |
| config. D | 21 | 0.5 | strong |
| config. E | 25 | 0.2 | strong |
Note that the 90th discretised intensity percentile obtained for the digital phantom may differ from the above reference value depending on the software implementation used to compute it. For example, some implementations were found to produce a value of 4.2 instead of 4 for this feature.
Maximum discretised intensity¶
3NCY
The maximum discretised intensity [Aerts2014] is equal to the highest discretised intensity present in \(\mathbf{X}_{d}\), i.e.:
By definition, \(F_{\mathit{ih.max}}=N_g\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 6 | — | very strong |
| config. A | 36 | 0.4 | strong |
| config. B | 32 | — | strong |
| config. C | 56 | 0.5 | strong |
| config. D | 32 | — | strong |
| config. E | 32 | — | strong |
Intensity histogram mode¶
AMMC
The mode of \(\mathbf{X}_{d}\) \(F_{\mathit{ih.mode}}\) is the most common discretised intensity present, i.e. the value \(i\) for with the highest count \(n_i\). The mode may not be uniquely defined. When the highest count is found in multiple bins, the value \(i\) of the bin closest to the mean discretised intensity is chosen as intensity histogram mode. In pathological cases with two such bins equidistant to the mean, the bin to the left of the mean is selected.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1 | — | very strong |
| config. A | 23 | — | strong |
| config. B | 20 | 0.3 | strong |
| config. C | 43 | 0.1 | strong |
| config. D | 20 | 0.4 | strong |
| config. E | 24 | 0.1 | strong |
Discretised intensity interquartile range¶
WR0O
The interquartile range (IQR) of \(\mathbf{X}_{d}\) is defined as:
\(P_{25}\) and \(P_{75}\) are the 25th and 75th percentile of \(\mathbf{X}_{d}\), respectively.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 3 | — | very strong |
| config. A | 2 | — | strong |
| config. B | 2 | — | strong |
| config. C | 3 | 0.21 | strong |
| config. D | 2 | 0.06 | strong |
| config. E | 1 | 0.06 | strong |
Discretised intensity range¶
5Z3W
The discretised intensity range [Aerts2014] is defined as:
For fixed bin number discretisation, the discretised intensity range equals \(N_g\) by definition.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 5 | — | very strong |
| config. A | 35 | 0.4 | strong |
| config. B | 31 | — | strong |
| config. C | 53 | 0.6 | strong |
| config. D | 31 | — | strong |
| config. E | 31 | — | strong |
Intensity histogram mean absolute deviation¶
D2ZX
The mean absolute deviation [Aerts2014] is a measure of dispersion from the mean of \(\mathbf{X}_{d}\):
Here \(\mu=F_{\mathit{ih.mean}}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1.55 | — | very strong |
| config. A | 2.94 | 0.06 | strong |
| config. B | 2.67 | 0.03 | strong |
| config. C | 6.32 | 0.15 | strong |
| config. D | 3.15 | 0.05 | strong |
| config. E | 3.69 | 0.1 | strong |
Intensity histogram robust mean absolute deviation¶
WRZB
Intensity histogram mean absolute deviation may be affected by outliers. To increase robustness, the set of discretised intensities under consideration can be restricted to those which are closer to the center of the distribution. Let
In short, \(\mathbf{X}_{d,10-90}\) is the set of \(N_{v,10-90}\leq N_v\) voxels in \(\mathbf{X}_{d}\) whose discretised intensities fall in the interval bounded by the 10th and 90th percentiles of \(\mathbf{X}_{d}\). The robust mean absolute deviation is then:
\(\overline{X}_{d,10-90}\) denotes the sample mean of \(\mathbf{X}_{d,10-90}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1.11 | — | very strong |
| config. A | 1.18 | 0.04 | strong |
| config. B | 1.03 | 0.03 | moderate |
| config. C | 2.59 | 0.14 | strong |
| config. D | 1.33 | 0.06 | strong |
| config. E | 1.46 | 0.09 | moderate |
Intensity histogram median absolute deviation¶
4RNL
Histogram median absolute deviation is conceptually similar to histogram mean absolute deviation, but measures dispersion from the median instead of mean. Thus:
Here, median \(M = F_{\mathit{ih.median}}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1.15 | — | very strong |
| config. A | 2.58 | 0.05 | strong |
| config. B | 2.28 | 0.02 | strong |
| config. C | 4.75 | 0.12 | strong |
| config. D | 2.41 | 0.04 | strong |
| config. E | 2.89 | 0.07 | strong |
Intensity histogram coefficient of variation¶
CWYJ
The coefficient of variation measures the dispersion of the discretised intensity distribution. It is defined as:
Here \(\sigma={F_{\mathit{ih.var}}}^{1/2}\) and \(\mu=F_{\mathit{ih.mean}}\) are the standard deviation and mean of the discretised intensity distribution, respectively.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.812 | — | very strong |
| config. A | 0.227 | 0.004 | strong |
| config. B | 0.229 | 0.004 | strong |
| config. C | 0.234 | 0.005 | strong |
| config. D | 0.252 | 0.006 | strong |
| config. E | 0.254 | 0.006 | strong |
Intensity histogram quartile coefficient of dispersion¶
SLWD
The quartile coefficient of dispersion is a more robust alternative to the intensity histogram coefficient of variance. It is defined as:
\(P_{25}\) and \(P_{75}\) are the 25th and 75th percentile of \(\mathbf{X}_{d}\), respectively.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.6 | — | very strong |
| config. A | 0.0455 | — | strong |
| config. B | 0.05 | 0.0005 | strong |
| config. C | 0.0361 | 0.0027 | strong |
| config. D | 0.05 | 0.0021 | strong |
| config. E | 0.0213 | 0.0015 | strong |
Discretised intensity entropy¶
TLU2
Entropy [Aerts2014] is an information-theoretic concept that gives a metric for the information contained within \(\mathbf{X}_{d}\). The particular metric used is Shannon entropy, which is defined as:
Note that entropy can only be meaningfully defined for discretised intensities as it will tend to \(-\log_2 N_v\) for continuous intensity distributions.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1.27 | — | very strong |
| config. A | 3.36 | 0.03 | very strong |
| config. B | 3.16 | 0.01 | strong |
| config. C | 3.73 | 0.04 | strong |
| config. D | 2.94 | 0.01 | strong |
| config. E | 3.22 | 0.02 | strong |
Discretised intensity uniformity¶
BJ5W
Uniformity [Aerts2014] of \(\mathbf{X}_{d}\) is defined as:
For histograms where most intensities are contained in a single bin, uniformity approaches \(1\). The lower bound is \(1/N_{g}\).
Note that this feature is sometimes referred to as energy.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.512 | — | very strong |
| config. A | 0.15 | 0.002 | very strong |
| config. B | 0.174 | 0.001 | strong |
| config. C | 0.14 | 0.003 | strong |
| config. D | 0.229 | 0.003 | strong |
| config. E | 0.184 | 0.001 | strong |
Maximum histogram gradient¶
12CE
The histogram gradient \(\mathbf{H}'\) of intensity histogram \(\mathbf{H}\) can be calculated as:
Histogram \(\mathbf{H}\) should be non-sparse, i.e. bins where \(n_i=0\) should not be omitted. Ostensibly, the histogram gradient can be calculated in different ways. The method above has the advantages of being easy to implement and leading to a gradient \(\mathbf{H}'\) with same size as \(\mathbf{H}\). This helps maintain a direct correspondence between the discretised intensities in \(\mathbf{H}\) and the bins of \(\mathbf{H}'\). The maximum histogram gradient [VanDijk2016] is:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 8 | — | very strong |
| config. A | \(1.1 \times 10^{4}\) | 100 | strong |
| config. B | \(3.22 \times 10^{3}\) | 50 | strong |
| config. C | \(4.75 \times 10^{3}\) | 30 | strong |
| config. D | \(7.26 \times 10^{3}\) | 200 | strong |
| config. E | \(6.01 \times 10^{3}\) | 130 | strong |
Maximum histogram gradient intensity¶
8E6O
The maximum histogram gradient intensity [VanDijk2016] \(F_{\mathit{ih.max.grad.gl}}\) is the discretised intensity corresponding to the maximum histogram gradient, i.e. the value \(i\) in \(\mathbf{H}\) for which \(\mathbf{H}'\) is maximal.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 3 | — | strong |
| config. A | 21 | — | strong |
| config. B | 19 | 0.3 | strong |
| config. C | 41 | — | strong |
| config. D | 19 | 0.4 | strong |
| config. E | 23 | 0.2 | moderate |
Minimum histogram gradient¶
VQB3
The minimum histogram gradient [VanDijk2016] is:
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | \(-\)50 | — | very strong |
| config. A | \(-1.01 \times 10^{4}\) | 100 | strong |
| config. B | \(-3.02 \times 10^{3}\) | 50 | strong |
| config. C | \(-4.68 \times 10^{3}\) | 50 | strong |
| config. D | \(-6.67 \times 10^{3}\) | 230 | strong |
| config. E | \(-6.11 \times 10^{3}\) | 180 | strong |
Minimum histogram gradient intensity¶
RHQZ
The minimum histogram gradient intensity [VanDijk2016] \(F_{\mathit{ih.min.grad.gl}}\) is the discretised intensity corresponding to the minimum histogram gradient, i.e. the value \(i\) in \(\mathbf{H}\) for which \(\mathbf{H}'\) is minimal.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 1 | — | strong |
| config. A | 24 | — | strong |
| config. B | 22 | 0.3 | strong |
| config. C | 44 | — | strong |
| config. D | 22 | 0.4 | strong |
| config. E | 25 | 0.2 | strong |
Intensity-volume histogram features¶
P88C
The (cumulative) intensity-volume histogram (IVH) of the set \(\mathbf{X}_{gl}\) of voxel intensities in the ROI intensity mask describes the relationship between discretised intensity \(i\) and the fraction of the volume containing at least intensity \(i\), \(\nu\) [ElNaqa2009].
Depending on the imaging modality, the calculation of IVH features requires discretising \(\mathbf{X}_{gl}\) to generate a new voxel set \(\mathbf{X}_{d,gl}\) with discretised intensities. Moreover, the total range \(\mathbf{G}\) of discretised intensities and the discretisation interval \(w_d\) should be provided or determined. The total range \(\mathbf{G}\) determines the range of discretised intensities to be included in the IVH, whereas the discretisation interval determines the intensity difference between adjacent discretised intensities in the IVH.
Recommendations for discretisation parameters differ depending on what type of data the image represents, and how it is represented. These recommendations are described below.
Discrete calibrated image intensities¶
Some imaging modalities by default generate voxels with calibrated, discrete intensities – for example CT. In this case, the discretised ROI voxel set \(\mathbf{X}_{d,gl}=\mathbf{X}_{gl}\), i.e. no discretisation required. If a re-segmentation range is provided (see Section Re-segmentation), the total range \(\mathbf{G}\) is equal to the re-segmentation range. In the case of a half-open re-segmentation range, the upper limit of the range is \(\text{max}(\mathbf{X}_{gl})\). When no range is provided, \(\mathbf{G}=[\text{min}(\mathbf{X}_{gl}),\text{max}(\mathbf{X}_{gl})]\). The discretisation interval is \(w_d=1\).
Continuous calibrated image intensities¶
Imaging with calibrated, continuous intensities such as PET requires discretisation to determine the IVH, while preserving the quantitative intensity information. The use of a fixed bin size discretisation method is thus recommended (see Intensity discretisation). This method requires a minimum intensity \(X_{gl,min}\), a maximum intensity \(X_{gl,max}\) and the bin width \(w_b\). If a re-segmentation range is defined (see Re-segmentation), \(X_{gl,min}\) is set to the lower bound of the re-segmentation range and \(X_{gl,max}\) to the upper bound; otherwise \(X_{gl,min} = \text{min}(\mathbf{X}_{gl})\) and \(X_{gl,max} = \text{max}(\mathbf{X}_{gl})\) (i.e. the minimum and maximum intensities in the imaging volume prior to discretisation). The bin width \(w_b\) is modality dependent, but should be small relative to the intensity range, e.g. 0.10 SUV for 18F-FDG-PET.
Next, fixed bin size discretisation produces the voxel set \(\mathbf{X}_{d}\) of bin numbers, which needs to be converted to bin centers in order to maintain a direct relationship with the original intensities. We thus replace bin numbers \(\mathbf{X}_{d}\) with the intensity corresponding to the bin center:
The total range is then \(\mathbf{G}=[X_{gl,min}+0.5w_b, X_{gl,max}-0.5w_b]\). In this case, the discretisation interval matches the bin width, i.e. \(w_d=w_b\).
Arbitrary intensity units¶
Some imaging modalities, such as many MRI sequences, produce arbitrary intensities. In such cases, a fixed bin number discretisation method with \(N_g=1000\) bins is recommended (see Intensity discretisation). The discretisation bin width is \(w_b=\left(X_{gl,max}-X_{gl,min}\right)/N_g\), with \(X_{gl,max}=\text{max}\left(\mathbf{X}_{gl}\right)\) and \(X_{gl,min}=\text{min}\left(\mathbf{X}_{gl}\right)\), as re-segmentation ranges generally cannot be provided for non-calibrated intensities. The fixed bin number discretisation produces the voxel set \(\mathbf{X}_{d} \in \{1,2,\ldots,N_g\}\). Because of the lack of calibration, \(\mathbf{X}_{d,gl}=\mathbf{X}_{d}\), and consequentially the discretisation interval is \(w_d=1\) and the total range is \(\mathbf{G}=[1,N_g]\)
Calculating the IV histogram¶
We use \(\mathbf{X}_{d,gl}\) to calculate fractional volumes and fractional intensities.
As voxels for the same image stack generally all have the same dimensions, we may define fractional volume \(\nu\) for discretised intensity \(i\):
Here \(\left[\ldots\right]\) is an Iverson bracket, yielding \(1\) if the condition is true and \(0\) otherwise. In essence, we count the voxels containing a discretised intensity smaller than \(i\), divide by the total number of voxels, and then subtract this volume fraction to find \(\nu_i\).
The intensity fraction \(\gamma\) for discretised intensity \(i\) in the range \(\mathbf{G}\) is calculated as:
Note that intensity fractions are also calculated for discretised intensities that are absent in \(\mathbf{X}_{d,gl}\). For example intensities 2 and 5 are absent in the digital phantom (see Reference data sets Chapter), but are still evaluated to determine both the fractional volume and the intensity fraction. An example IVH for the digital phantom is shown in Table 71.
| \(i\) | \(\gamma\) | \(\nu\) |
|---|---|---|
| 1 | 0.0 | 1.000 |
| 2 | 0.2 | 0.324 |
| 3 | 0.4 | 0.324 |
| 4 | 0.6 | 0.311 |
| 5 | 0.8 | 0.095 |
| 6 | 1.0 | 0.095 |
Aggregating features¶
We recommend calculating intensity-volume histogram features using the 3D volume (DHQ4). Computing features per slice and subsequently averaging (3IDG) is not recommended.
Volume at intensity fraction¶
BC2M
The volume at intensity fraction \(V_x\) is the largest volume fraction \(\nu\) that has an intensity fraction \(\gamma\) of at least \(x\%\). This differs from conceptually similar dose-volume histograms used in radiotherapy planning, where \(V_{10}\) would indicate the volume fraction receiving at least 10 Gy planned dose. [ElNaqa2009] defined both \(V_{10}\) and \(V_{90}\) as features. In the context of this work, these two features are defined as \(F_{\mathit{ivh.V10}}\) and \(F_{\mathit{ivh.V90}}\), respectively.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.324 | — | very strong |
| config. A | 0.978 | 0.001 | strong |
| config. B | 0.977 | 0.001 | strong |
| config. C | 0.998 | 0.001 | moderate |
| config. D | 0.972 | 0.003 | strong |
| config. E | 0.975 | 0.002 | strong |
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.0946 | — | very strong |
| config. A | \(6.98 \times 10^{-5}\) | \(1.03 \times 10^{-5}\) | strong |
| config. B | \(7.31 \times 10^{-5}\) | \(1.03 \times 10^{-5}\) | strong |
| config. C | 0.000152 | \(2 \times 10^{-5}\) | strong |
| config. D | \(9 \times 10^{-5}\) | 0.000415 | strong |
| config. E | 0.000157 | 0.000248 | strong |
Intensity at volume fraction¶
GBPN
The intensity at volume fraction \(I_x\) is the minimum discretised intensity \(i\) present in at most \(x\%\) of the volume. [ElNaqa2009] defined both \(I_{10}\) and \(I_{90}\) as features. In the context of this work, these two features are defined as \(F_{\mathit{ivh.I10}}\) and \(F_{\mathit{ivh.I90}}\), respectively.
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 5 | — | very strong |
| config. A | 96 | — | strong |
| config. B | 92 | — | strong |
| config. C | 88.8 | 0.2 | moderate |
| config. D | 87 | 0.1 | strong |
| config. E | 770 | 5 | moderate |
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 2 | — | very strong |
| config. A | \(-\)128 | 8 | strong |
| config. B | \(-\)135 | 8 | strong |
| config. C | \(-\)421 | 14 | strong |
| config. D | \(-\)303 | 20 | strong |
| config. E | 399 | 17 | moderate |
Volume fraction difference between intensity fractions¶
DDTU
This feature is the difference between the volume fractions at two different intensity fractions, e.g. \(V_{10}-V_{90}\) [ElNaqa2009]. In the context of this work, this feature is defined as \(F_{\mathit{ivh.V10minusV90}}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 0.23 | — | very strong |
| config. A | 0.978 | 0.001 | strong |
| config. B | 0.977 | 0.001 | strong |
| config. C | 0.997 | 0.001 | strong |
| config. D | 0.971 | 0.001 | strong |
| config. E | 0.974 | 0.001 | strong |
Intensity fraction difference between volume fractions¶
CNV2
This feature is the difference between discretised intensities at two different fractional volumes, e.g. \(I_{10} - I_{90}\) [ElNaqa2009]. In the context of this work, this feature is defined as \(F_{\mathit{ivh.I10minusI90}}\).
| data | value | tol. | consensus |
|---|---|---|---|
| dig. phantom | 3 | — | very strong |
| config. A | 224 | 8 | strong |
| config. B | 227 | 8 | strong |
| config. C | 510 | 14 | strong |
| config. D | 390 | 20 | strong |
| config. E | 371 | 13 | moderate |
Area under the IVH curve¶
9CMM
Note: This feature currently has no reference values and should not be used.
The area under the IVH curve \(F_{\mathit{ivh.auc}}\) was defined by [VanVelden2011]. The area under the IVH curve can be approximated by calculating the Riemann sum using the trapezoidal rule. Note that if there is only one discretised intensity in the ROI, we define the area under the IVH curve \(F_{\mathit{ivh.auc}}=0\).
Grey level co-occurrence based features¶
LFYI
In image analysis, texture is one of the defining sets of features. Texture features were originally designed to assess surface texture in 2D images. Texture analysis is however not restricted to 2D slices and can be extended to 3D objects. Image intensities are generally discretised before calculation of texture features (see Intensity discretisation).
The grey level co-occurrence matrix (GLCM) is a matrix that expresses how combinations of discretised intensities (grey levels) of neighbouring pixels, or voxels in a 3D volume, are distributed along one of the image directions. Generally, the neighbourhood for GLCM is a 26-connected neighbourhood in 3D and a 8-connected neighbourhood in 2D. Thus, in 3D there are 13 unique direction vectors within the neighbourhood for Chebyshev distance \(\delta=1\), i.e. \((0,0,1)\), \((0,1,0)\), \((1,0,0)\), \((0,1,1)\), \((0,1,-1)\), \((1,0,1)\), \((1,0,-1)\), \((1,1,0)\), \((1,-1,0)\), \((1,1,1)\), \((1,1,-1)\), \((1,-1,1)\) and \((1,-1,-1)\), whereas in 2D the direction vectors are \((1,0,0)\), \((1,1,0)\), \((0,1,0)\) and \((-1,1,0)\).
A GLCM is calculated for each direction vector, as follows. Let \(\mathbf{M}_{\mathbf{m}}\) be the \(N_g \times N_g\) grey level co-occurrence matrix, with \(N_g\) the number of discretised grey levels present in the ROI intensity mask, and \(\mathbf{m}\) the particular direction vector. Element \((i,j)\) of the GLCM contains the frequency at which combinations of discretised grey levels \(i\) and \(j\) occur in neighbouring voxels along direction \(\mathbf{m}_{+}=\mathbf{m}\) and along direction \(\mathbf{m}_{-}= -\mathbf{m}\). Then, \(\mathbf{M}_{\mathbf{m}} = \mathbf{M}_{\mathbf{m}_{+}} + \mathbf{M}_{\mathbf{m}_{-}} = \mathbf{M}_{\mathbf{m}_{+}} + \mathbf{M}_{\mathbf{m}_{+}}^T\) [Haralick1973]. As a consequence the GLCM matrix \(\mathbf{M}_{\mathbf{m}}\) is symmetric. An example of the calculation of a GLCM is shown in Fig. 10. Corresponding grey level co-occurrence matrices for each direction are shown in Fig. 11.

Fig. 10 Grey levels (a) and corresponding grey level co-occurrence matrices for the 0◦ (b) and 180◦ directions (c). In vector notation these directions are \(\mathbf{m_{+}} = (1, 0)\) and \(\mathbf{m_{-}}\) = (−1, 0). To calculate the symmetrical co-occurrence matrix \(\mathbf{M}_{\mathbf{m}}\) both matrices are summed by element.

Fig. 11 Grey level co-occurrence matrices for the 0◦ (a), 45◦ (b), 90◦ (c) and 135◦ (d) directions. In vector notation these directions are \(\mathbf{m} = (1, 0)\), \(\mathbf{m} = (1, 1)\), \(\mathbf{m} = (0, 1)\) and \(\mathbf{m} = (−1, 1)\), respectively.
GLCM features rely on the probability distribution for the elements of the GLCM. Let us consider \(\mathbf{M}_{\mathbf{m}=(1,0)}\) from the example, as shown in Fig. 12. We derive a probability distribution for grey level co-occurrences, \(\mathbf{P}_{\mathbf{m}}\), by normalising \(\mathbf{M}_{\mathbf{m}}\) by the sum of its elements. Each element \(p_{ij}\) of \(\mathbf{P}_{\mathbf{m}}\) is then the joint probability of grey levels \(i\) and \(j\) occurring in neighbouring voxels along direction \(\mathbf{m}\). Then \(p_{i.} = \sum_{j=1}^{N_g} p_{ij}\) is the row marginal probability, and \(p_{.j}=\sum_{i=1}^{N_g} p_{ij}\) is the column marginal probability. As \(\mathbf{P}_{\mathbf{m}}\) is by definition symmetric, \(p_{i.} = p_{.j}\). Furthermore, let us consider diagonal and cross-diagonal probabilities \(p_{i-j}\) and \(p_{i+j}\) [Haralick1973][Unser1986]:
Here, \(\left[\ldots\right]\) is an Iverson bracket, which equals \(1\) when the condition within the brackets is true and \(0\) otherwise. In effect we select only combinations of elements \((i,j)\) for which the condition holds.
It should be noted that while a distance \(\delta=1\) is commonly used for GLCM, other distances are possible. However, this does not change the number of For example, for \(\delta=3\) (in 3D) the voxels at \((0,0,3)\), \((0,3,0)\), \((3,0,0)\), \((0,3,3)\), \((0,3,-3)\), \((3,0,3)\), \((3,0,-3)\), \((3,3,0)\), \((3,-3,0)\), \((3,3,3)\), \((3,3,-3)\), \((3,-3,3)\) and \((3,-3,-3)\) from the center voxel are considered.

Fig. 12 Grey level co-occurrence matrix for the 0◦ direction (a); its corresponding probability matrix \(\mathbf{P}_{\mathbf{m}} = (1,0)\) with marginal probabilities \(p_{i.}\). and \(p_{.j}\); the diagonal probabilities \(p_{i-j}\) (c); and the cross-diagonal probabilities \(p_{i+j}\) (d). Discrepancies in panels b, c, and d are due to rounding errors caused by showing only two decimal places. Also, note that due to GLCM symmetry marginal probabilities \(p_{i.}\). and \(p_{.j}\) are the same in both row and column margins of panel b.
Aggregating features¶
To improve rotational invariance, GLCM feature values are computed by aggregating information from the different underlying directional matrices [Depeursinge2017a]. Five methods can be used to aggregate GLCMs and arrive at a single feature value. A schematic example is shown in Fig. 13. A feature may be aggregated as follows:
- Features are computed from each 2D directional matrix and averaged over 2D directions and slices (BTW3).
- Features are computed from a single matrix after merging 2D directional matrices per slice, and then averaged over slices (SUJT).
- Features are computed from a single matrix after merging 2D directional matrices per direction, and then averaged over directions (JJUI).
- The feature is computed from a single matrix after merging all 2D directional matrices (ZW7Z).
- Features are computed from each 3D directional matrix and averaged over the 3D directions (ITBB).
- The feature is computed from a single matrix after merging all 3D directional matrices (IAZD).
In methods 2,3,4 and 6, matrices are merged by summing the co-occurrence counts in each matrix element \((i,j)\) over the different matrices. Probability distributions are subsequently calculated for the merged GLCM, which is then used to calculate GLCM features. Feature values may dependent strongly on the aggregation method.
Fig. 13 Approaches to calculating grey level co-occurrence matrix-based features. M∆k are texture matrices calculated for direction \(\delta\) in slice \(k\) (if applicable), and \(f_{\delta k}\) is the corresponding feature value. In (b-d) and (e) the matrices are merged prior to feature calculation.
Distances and distance weighting¶
The default neighbourhood includes all voxels within Chebyshev distance \(1\). The corresponding direction vectors are multiplied by the desired distance \(\delta\). From a technical point-of-view, direction vectors may also be determined differently, using any distance norm. In this case, direction vectors are the vectors to the voxels at \(\delta\), or between \(\delta\) and \(\delta-1\) for the Euclidean norm. Such usage is however rare and we caution against it due to potential reproducibility issues.
GLCMs may be weighted for distance by multiplying \(\mathbf{M}\) with a weighting factor \(w\). By default \(w=1\), but \(w\) may also be an inverse distance function to weight each GLCM, e.g. \(w=\|\mathbf{m}\|^{-1}\) or \(w=\exp(-\|\mathbf{m}\|^2)\) [VanGriethuysen2017], with \(\|\mathbf{m}\|\) the length of direction vector \(m\). Whether distance weighting yields different feature values depends on several factors. When aggregating the feature values, matrices have to be merged first, otherwise weighting has no effect. Also, it has no effect if the default neighbourhood is used and the Chebyshev norm is using for weighting. Nor does weighting have an effect if either Manhattan or Chebyshev norms are used both for constructing a non-default neighbourhood and for weighting. Weighting may furthermore have no effect for distance \(\delta=1\), dependent on distance norms. Because of these exceptions, we recommend against using distance weighting for GLCM.
Joint maximum¶
GYBY
Joint maximum [Haralick1979] is the probability corresponding to the most common grey level co-occurrence in the GLCM:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.519 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.512 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.489 | — | strong |
| dig. phantom | 2.5D, merged | 0.492 | — | strong |
| dig. phantom | 3D, averaged | 0.503 | — | very strong |
| dig. phantom | 3D, merged | 0.509 | — | very strong |
| config. A | 2D, averaged | 0.109 | 0.001 | strong |
| config. A | 2D, slice-merged | 0.109 | 0.001 | strong |
| config. A | 2.5D, direction-merged | 0.0943 | 0.0008 | strong |
| config. A | 2.5D, merged | 0.0943 | 0.0008 | strong |
| config. B | 2D, averaged | 0.156 | 0.002 | strong |
| config. B | 2D, slice-merged | 0.156 | 0.002 | strong |
| config. B | 2.5D, direction-merged | 0.126 | 0.002 | strong |
| config. B | 2.5D, merged | 0.126 | 0.002 | strong |
| config. C | 3D, averaged | 0.111 | 0.002 | strong |
| config. C | 3D, merged | 0.111 | 0.002 | very strong |
| config. D | 3D, averaged | 0.232 | 0.007 | strong |
| config. D | 3D, merged | 0.232 | 0.007 | strong |
| config. E | 3D, averaged | 0.153 | 0.003 | moderate |
| config. E | 3D, merged | 0.153 | 0.003 | strong |
Joint average¶
60VM
Joint average [Unser1986] is the grey level weighted sum of joint probabilities:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 2.14 | — | very strong |
| dig. phantom | 2D, slice-merged | 2.14 | — | strong |
| dig. phantom | 2.5D, direction-merged | 2.2 | — | strong |
| dig. phantom | 2.5D, merged | 2.2 | — | strong |
| dig. phantom | 3D, averaged | 2.14 | — | very strong |
| dig. phantom | 3D, merged | 2.15 | — | very strong |
| config. A | 2D, averaged | 20.6 | 0.1 | strong |
| config. A | 2D, slice-merged | 20.6 | 0.1 | strong |
| config. A | 2.5D, direction-merged | 21.3 | 0.1 | strong |
| config. A | 2.5D, merged | 21.3 | 0.1 | strong |
| config. B | 2D, averaged | 18.7 | 0.3 | strong |
| config. B | 2D, slice-merged | 18.7 | 0.3 | strong |
| config. B | 2.5D, direction-merged | 19.2 | 0.3 | strong |
| config. B | 2.5D, merged | 19.2 | 0.3 | strong |
| config. C | 3D, averaged | 39 | 0.2 | strong |
| config. C | 3D, merged | 39 | 0.2 | strong |
| config. D | 3D, averaged | 18.9 | 0.5 | strong |
| config. D | 3D, merged | 18.9 | 0.5 | strong |
| config. E | 3D, averaged | 22.1 | 0.3 | strong |
| config. E | 3D, merged | 22.1 | 0.3 | strong |
Joint variance¶
UR99
The joint variance [Unser1986], which is also called sum of squares [Haralick1973], is defined as:
Here \(\mu\) is equal to the value of \(F_{\mathit{cm.joint.avg}}\), which was defined above.
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 2.69 | — | very strong |
| dig. phantom | 2D, slice-merged | 2.71 | — | strong |
| dig. phantom | 2.5D, direction-merged | 3.22 | — | strong |
| dig. phantom | 2.5D, merged | 3.24 | — | strong |
| dig. phantom | 3D, averaged | 3.1 | — | very strong |
| dig. phantom | 3D, merged | 3.13 | — | very strong |
| config. A | 2D, averaged | 27 | 0.4 | strong |
| config. A | 2D, slice-merged | 27 | 0.4 | strong |
| config. A | 2.5D, direction-merged | 18.6 | 0.5 | strong |
| config. A | 2.5D, merged | 18.6 | 0.5 | strong |
| config. B | 2D, averaged | 21 | 0.3 | strong |
| config. B | 2D, slice-merged | 21 | 0.3 | strong |
| config. B | 2.5D, direction-merged | 14.2 | 0.1 | strong |
| config. B | 2.5D, merged | 14.2 | 0.1 | strong |
| config. C | 3D, averaged | 73.7 | 2 | strong |
| config. C | 3D, merged | 73.8 | 2 | very strong |
| config. D | 3D, averaged | 17.6 | 0.4 | strong |
| config. D | 3D, merged | 17.6 | 0.4 | strong |
| config. E | 3D, averaged | 24.4 | 0.9 | moderate |
| config. E | 3D, merged | 24.4 | 0.9 | strong |
Joint entropy¶
TU9B
Joint entropy [Haralick1973] is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 2.05 | — | very strong |
| dig. phantom | 2D, slice-merged | 2.24 | — | strong |
| dig. phantom | 2.5D, direction-merged | 2.48 | — | strong |
| dig. phantom | 2.5D, merged | 2.61 | — | strong |
| dig. phantom | 3D, averaged | 2.4 | — | very strong |
| dig. phantom | 3D, merged | 2.57 | — | very strong |
| config. A | 2D, averaged | 5.82 | 0.04 | strong |
| config. A | 2D, slice-merged | 5.9 | 0.04 | strong |
| config. A | 2.5D, direction-merged | 5.78 | 0.04 | strong |
| config. A | 2.5D, merged | 5.79 | 0.04 | strong |
| config. B | 2D, averaged | 5.26 | 0.02 | strong |
| config. B | 2D, slice-merged | 5.45 | 0.01 | strong |
| config. B | 2.5D, direction-merged | 5.45 | 0.01 | strong |
| config. B | 2.5D, merged | 5.46 | 0.01 | strong |
| config. C | 3D, averaged | 6.39 | 0.06 | strong |
| config. C | 3D, merged | 6.42 | 0.06 | very strong |
| config. D | 3D, averaged | 4.95 | 0.03 | strong |
| config. D | 3D, merged | 4.96 | 0.03 | strong |
| config. E | 3D, averaged | 5.6 | 0.03 | strong |
| config. E | 3D, merged | 5.61 | 0.03 | strong |
Difference average¶
TF7R
The difference average [Unser1986] for the diagonal probabilities is defined as:
By definition difference average is equivalent to the dissimilarity feature [VanGriethuysen2017].
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 1.42 | — | very strong |
| dig. phantom | 2D, slice-merged | 1.4 | — | strong |
| dig. phantom | 2.5D, direction-merged | 1.46 | — | strong |
| dig. phantom | 2.5D, merged | 1.44 | — | strong |
| dig. phantom | 3D, averaged | 1.43 | — | very strong |
| dig. phantom | 3D, merged | 1.38 | — | very strong |
| config. A | 2D, averaged | 1.58 | 0.03 | strong |
| config. A | 2D, slice-merged | 1.57 | 0.03 | strong |
| config. A | 2.5D, direction-merged | 1.35 | 0.03 | strong |
| config. A | 2.5D, merged | 1.35 | 0.03 | strong |
| config. B | 2D, averaged | 1.81 | 0.01 | strong |
| config. B | 2D, slice-merged | 1.81 | 0.01 | strong |
| config. B | 2.5D, direction-merged | 1.47 | 0.01 | strong |
| config. B | 2.5D, merged | 1.47 | 0.01 | strong |
| config. C | 3D, averaged | 2.17 | 0.05 | strong |
| config. C | 3D, merged | 2.16 | 0.05 | strong |
| config. D | 3D, averaged | 1.29 | 0.01 | strong |
| config. D | 3D, merged | 1.29 | 0.01 | strong |
| config. E | 3D, averaged | 1.7 | 0.01 | strong |
| config. E | 3D, merged | 1.7 | 0.01 | strong |
Difference variance¶
D3YU
The difference variance for the diagonal probabilities [Haralick1973] is defined as:
Here \(\mu\) is equal to the value of difference average.
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 2.9 | — | very strong |
| dig. phantom | 2D, slice-merged | 3.06 | — | strong |
| dig. phantom | 2.5D, direction-merged | 3.11 | — | strong |
| dig. phantom | 2.5D, merged | 3.23 | — | strong |
| dig. phantom | 3D, averaged | 3.06 | — | very strong |
| dig. phantom | 3D, merged | 3.21 | — | very strong |
| config. A | 2D, averaged | 4.94 | 0.19 | strong |
| config. A | 2D, slice-merged | 4.96 | 0.19 | strong |
| config. A | 2.5D, direction-merged | 4.12 | 0.2 | strong |
| config. A | 2.5D, merged | 4.14 | 0.2 | strong |
| config. B | 2D, averaged | 7.74 | 0.05 | strong |
| config. B | 2D, slice-merged | 7.76 | 0.05 | strong |
| config. B | 2.5D, direction-merged | 6.48 | 0.06 | strong |
| config. B | 2.5D, merged | 6.48 | 0.06 | strong |
| config. C | 3D, averaged | 14.4 | 0.5 | strong |
| config. C | 3D, merged | 14.4 | 0.5 | strong |
| config. D | 3D, averaged | 5.37 | 0.11 | strong |
| config. D | 3D, merged | 5.38 | 0.11 | strong |
| config. E | 3D, averaged | 8.22 | 0.06 | strong |
| config. E | 3D, merged | 8.23 | 0.06 | strong |
Difference entropy¶
NTRS
The difference entropy for the diagonal probabilities [Haralick1973] is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 1.4 | — | very strong |
| dig. phantom | 2D, slice-merged | 1.49 | — | strong |
| dig. phantom | 2.5D, direction-merged | 1.61 | — | strong |
| dig. phantom | 2.5D, merged | 1.67 | — | strong |
| dig. phantom | 3D, averaged | 1.56 | — | very strong |
| dig. phantom | 3D, merged | 1.64 | — | very strong |
| config. A | 2D, averaged | 2.27 | 0.03 | strong |
| config. A | 2D, slice-merged | 2.28 | 0.03 | strong |
| config. A | 2.5D, direction-merged | 2.16 | 0.03 | strong |
| config. A | 2.5D, merged | 2.16 | 0.03 | strong |
| config. B | 2D, averaged | 2.35 | 0.01 | strong |
| config. B | 2D, slice-merged | 2.38 | 0.01 | strong |
| config. B | 2.5D, direction-merged | 2.24 | 0.01 | moderate |
| config. B | 2.5D, merged | 2.24 | 0.01 | strong |
| config. C | 3D, averaged | 2.64 | 0.03 | strong |
| config. C | 3D, merged | 2.64 | 0.03 | very strong |
| config. D | 3D, averaged | 2.13 | 0.01 | strong |
| config. D | 3D, merged | 2.14 | 0.01 | strong |
| config. E | 3D, averaged | 2.39 | 0.01 | strong |
| config. E | 3D, merged | 2.4 | 0.01 | strong |
Sum average¶
ZGXS
The sum average for the cross-diagonal probabilities [Haralick1973] is defined as:
By definition, \(F_{\mathit{cm.sum.avg}} = 2 F_{\mathit{cm.joint.avg}}\) [VanGriethuysen2017].
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 4.28 | — | very strong |
| dig. phantom | 2D, slice-merged | 4.29 | — | strong |
| dig. phantom | 2.5D, direction-merged | 4.41 | — | strong |
| dig. phantom | 2.5D, merged | 4.41 | — | strong |
| dig. phantom | 3D, averaged | 4.29 | — | very strong |
| dig. phantom | 3D, merged | 4.3 | — | very strong |
| config. A | 2D, averaged | 41.3 | 0.1 | strong |
| config. A | 2D, slice-merged | 41.3 | 0.1 | strong |
| config. A | 2.5D, direction-merged | 42.7 | 0.1 | strong |
| config. A | 2.5D, merged | 42.7 | 0.1 | strong |
| config. B | 2D, averaged | 37.4 | 0.5 | strong |
| config. B | 2D, slice-merged | 37.4 | 0.5 | strong |
| config. B | 2.5D, direction-merged | 38.5 | 0.6 | strong |
| config. B | 2.5D, merged | 38.5 | 0.6 | strong |
| config. C | 3D, averaged | 78 | 0.3 | strong |
| config. C | 3D, merged | 78 | 0.3 | strong |
| config. D | 3D, averaged | 37.7 | 0.8 | strong |
| config. D | 3D, merged | 37.7 | 0.8 | strong |
| config. E | 3D, averaged | 44.3 | 0.4 | strong |
| config. E | 3D, merged | 44.3 | 0.4 | strong |
Sum variance¶
OEEB
The sum variance for the cross-diagonal probabilities [Haralick1973] is defined as:
Here \(\mu\) is equal to the value of sum average. Sum variance is mathematically identical to the cluster tendency feature [VanGriethuysen2017].
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 5.47 | — | very strong |
| dig. phantom | 2D, slice-merged | 5.66 | — | strong |
| dig. phantom | 2.5D, direction-merged | 7.48 | — | strong |
| dig. phantom | 2.5D, merged | 7.65 | — | strong |
| dig. phantom | 3D, averaged | 7.07 | — | very strong |
| dig. phantom | 3D, merged | 7.41 | — | very strong |
| config. A | 2D, averaged | 100 | 1 | strong |
| config. A | 2D, slice-merged | 100 | 1 | strong |
| config. A | 2.5D, direction-merged | 68.5 | 1.3 | strong |
| config. A | 2.5D, merged | 68.5 | 1.3 | strong |
| config. B | 2D, averaged | 72.1 | 1 | strong |
| config. B | 2D, slice-merged | 72.3 | 1 | strong |
| config. B | 2.5D, direction-merged | 48.1 | 0.4 | strong |
| config. B | 2.5D, merged | 48.1 | 0.4 | strong |
| config. C | 3D, averaged | 276 | 8 | strong |
| config. C | 3D, merged | 276 | 8 | very strong |
| config. D | 3D, averaged | 63.4 | 1.3 | strong |
| config. D | 3D, merged | 63.5 | 1.3 | strong |
| config. E | 3D, averaged | 86.6 | 3.3 | moderate |
| config. E | 3D, merged | 86.7 | 3.3 | strong |
Sum entropy¶
P6QZ
The sum entropy for the cross-diagonal probabilities [Haralick1973] is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 1.6 | — | very strong |
| dig. phantom | 2D, slice-merged | 1.79 | — | strong |
| dig. phantom | 2.5D, direction-merged | 2.01 | — | strong |
| dig. phantom | 2.5D, merged | 2.14 | — | strong |
| dig. phantom | 3D, averaged | 1.92 | — | very strong |
| dig. phantom | 3D, merged | 2.11 | — | very strong |
| config. A | 2D, averaged | 4.19 | 0.03 | strong |
| config. A | 2D, slice-merged | 4.21 | 0.03 | strong |
| config. A | 2.5D, direction-merged | 4.17 | 0.03 | strong |
| config. A | 2.5D, merged | 4.18 | 0.03 | strong |
| config. B | 2D, averaged | 3.83 | 0.01 | strong |
| config. B | 2D, slice-merged | 3.89 | 0.01 | strong |
| config. B | 2.5D, direction-merged | 3.91 | 0.01 | strong |
| config. B | 2.5D, merged | 3.91 | 0.01 | strong |
| config. C | 3D, averaged | 4.56 | 0.04 | strong |
| config. C | 3D, merged | 4.56 | 0.04 | very strong |
| config. D | 3D, averaged | 3.68 | 0.02 | strong |
| config. D | 3D, merged | 3.68 | 0.02 | strong |
| config. E | 3D, averaged | 3.96 | 0.02 | strong |
| config. E | 3D, merged | 3.97 | 0.02 | strong |
Angular second moment¶
8ZQL
The angular second moment [Haralick1973], which represents the energy of \(\mathbf{P}_{\Delta}\), is defined as:
This feature is also called energy [Unser1986][Aerts2014] and uniformity [Clausi2002].
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.368 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.352 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.286 | — | strong |
| dig. phantom | 2.5D, merged | 0.277 | — | strong |
| dig. phantom | 3D, averaged | 0.303 | — | very strong |
| dig. phantom | 3D, merged | 0.291 | — | very strong |
| config. A | 2D, averaged | 0.045 | 0.0008 | strong |
| config. A | 2D, slice-merged | 0.0446 | 0.0008 | strong |
| config. A | 2.5D, direction-merged | 0.0429 | 0.0007 | strong |
| config. A | 2.5D, merged | 0.0427 | 0.0007 | strong |
| config. B | 2D, averaged | 0.0678 | 0.0006 | strong |
| config. B | 2D, slice-merged | 0.0669 | 0.0006 | strong |
| config. B | 2.5D, direction-merged | 0.0581 | 0.0006 | strong |
| config. B | 2.5D, merged | 0.058 | 0.0006 | strong |
| config. C | 3D, averaged | 0.045 | 0.001 | strong |
| config. C | 3D, merged | 0.0447 | 0.001 | very strong |
| config. D | 3D, averaged | 0.11 | 0.003 | strong |
| config. D | 3D, merged | 0.109 | 0.003 | strong |
| config. E | 3D, averaged | 0.0638 | 0.0009 | strong |
| config. E | 3D, merged | 0.0635 | 0.0009 | strong |
Contrast¶
ACUI
Contrast assesses grey level variations [Haralick1973]. Hence elements of \(\mathbf{M}_{\Delta}\) that represent large grey level differences receive greater weight. Contrast is defined as [Clausi2002]:
Note that the original definition by [Haralick1973] is seemingly more complex, but rearranging and simplifying terms leads to the above formulation of contrast.
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 5.28 | — | very strong |
| dig. phantom | 2D, slice-merged | 5.19 | — | strong |
| dig. phantom | 2.5D, direction-merged | 5.39 | — | strong |
| dig. phantom | 2.5D, merged | 5.29 | — | strong |
| dig. phantom | 3D, averaged | 5.32 | — | very strong |
| dig. phantom | 3D, merged | 5.12 | — | very strong |
| config. A | 2D, averaged | 7.85 | 0.26 | strong |
| config. A | 2D, slice-merged | 7.82 | 0.26 | strong |
| config. A | 2.5D, direction-merged | 5.96 | 0.27 | strong |
| config. A | 2.5D, merged | 5.95 | 0.27 | strong |
| config. B | 2D, averaged | 11.9 | 0.1 | strong |
| config. B | 2D, slice-merged | 11.8 | 0.1 | strong |
| config. B | 2.5D, direction-merged | 8.66 | 0.09 | strong |
| config. B | 2.5D, merged | 8.65 | 0.09 | strong |
| config. C | 3D, averaged | 19.2 | 0.7 | strong |
| config. C | 3D, merged | 19.1 | 0.7 | very strong |
| config. D | 3D, averaged | 7.07 | 0.13 | strong |
| config. D | 3D, merged | 7.05 | 0.13 | strong |
| config. E | 3D, averaged | 11.1 | 0.1 | strong |
| config. E | 3D, merged | 11.1 | 0.1 | strong |
Dissimilarity¶
8S9J
Dissimilarity [Clausi2002] is conceptually similar to the contrast feature, and is defined as:
By definition dissimilarity is equivalent to the difference average feature [VanGriethuysen2017].
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 1.42 | — | very strong |
| dig. phantom | 2D, slice-merged | 1.4 | — | strong |
| dig. phantom | 2.5D, direction-merged | 1.46 | — | strong |
| dig. phantom | 2.5D, merged | 1.44 | — | strong |
| dig. phantom | 3D, averaged | 1.43 | — | very strong |
| dig. phantom | 3D, merged | 1.38 | — | very strong |
| config. A | 2D, averaged | 1.58 | 0.03 | strong |
| config. A | 2D, slice-merged | 1.57 | 0.03 | strong |
| config. A | 2.5D, direction-merged | 1.35 | 0.03 | strong |
| config. A | 2.5D, merged | 1.35 | 0.03 | strong |
| config. B | 2D, averaged | 1.81 | 0.01 | strong |
| config. B | 2D, slice-merged | 1.81 | 0.01 | strong |
| config. B | 2.5D, direction-merged | 1.47 | 0.01 | strong |
| config. B | 2.5D, merged | 1.47 | 0.01 | strong |
| config. C | 3D, averaged | 2.17 | 0.05 | strong |
| config. C | 3D, merged | 2.16 | 0.05 | very strong |
| config. D | 3D, averaged | 1.29 | 0.01 | strong |
| config. D | 3D, merged | 1.29 | 0.01 | strong |
| config. E | 3D, averaged | 1.7 | 0.01 | strong |
| config. E | 3D, merged | 1.7 | 0.01 | strong |
Inverse difference¶
IB1Z
Inverse difference is a measure of homogeneity [Clausi2002]. Grey level co-occurrences with a large difference in levels are weighed less, thus lowering the total feature value. The feature score is maximal if all grey levels are the same. Inverse difference is defined as:
The equation above may also be expressed in terms of diagonal probabilities [VanGriethuysen2017]:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.678 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.683 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.668 | — | strong |
| dig. phantom | 2.5D, merged | 0.673 | — | strong |
| dig. phantom | 3D, averaged | 0.677 | — | very strong |
| dig. phantom | 3D, merged | 0.688 | — | very strong |
| config. A | 2D, averaged | 0.581 | 0.003 | strong |
| config. A | 2D, slice-merged | 0.581 | 0.003 | strong |
| config. A | 2.5D, direction-merged | 0.605 | 0.003 | strong |
| config. A | 2.5D, merged | 0.605 | 0.003 | strong |
| config. B | 2D, averaged | 0.592 | 0.001 | strong |
| config. B | 2D, slice-merged | 0.593 | 0.001 | strong |
| config. B | 2.5D, direction-merged | 0.628 | 0.001 | strong |
| config. B | 2.5D, merged | 0.628 | 0.001 | strong |
| config. C | 3D, averaged | 0.582 | 0.004 | strong |
| config. C | 3D, merged | 0.583 | 0.004 | very strong |
| config. D | 3D, averaged | 0.682 | 0.003 | strong |
| config. D | 3D, merged | 0.682 | 0.003 | strong |
| config. E | 3D, averaged | 0.608 | 0.001 | moderate |
| config. E | 3D, merged | 0.608 | 0.001 | strong |
Normalised inverse difference¶
NDRX
[Clausi2002] suggested normalising inverse difference to improve classification ability. The normalised feature is then defined as:
Note that in Clausi’s definition, \(|i-j|^2/N_g^2\) is used instead of \(|i-j|/N_g\), which is likely an oversight, as this exactly matches the definition of the normalised inverse difference moment feature.
The equation may also be expressed in terms of diagonal probabilities [VanGriethuysen2017]:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.851 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.854 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.847 | — | strong |
| dig. phantom | 2.5D, merged | 0.85 | — | strong |
| dig. phantom | 3D, averaged | 0.851 | — | very strong |
| dig. phantom | 3D, merged | 0.856 | — | very strong |
| config. A | 2D, averaged | 0.961 | 0.001 | strong |
| config. A | 2D, slice-merged | 0.961 | 0.001 | strong |
| config. A | 2.5D, direction-merged | 0.966 | 0.001 | strong |
| config. A | 2.5D, merged | 0.966 | 0.001 | strong |
| config. B | 2D, averaged | 0.952 | 0.001 | strong |
| config. B | 2D, slice-merged | 0.952 | 0.001 | strong |
| config. B | 2.5D, direction-merged | 0.96 | 0.001 | strong |
| config. B | 2.5D, merged | 0.96 | 0.001 | strong |
| config. C | 3D, averaged | 0.966 | 0.001 | strong |
| config. C | 3D, merged | 0.966 | 0.001 | very strong |
| config. D | 3D, averaged | 0.965 | 0.001 | strong |
| config. D | 3D, merged | 0.965 | 0.001 | strong |
| config. E | 3D, averaged | 0.955 | 0.001 | strong |
| config. E | 3D, merged | 0.955 | 0.001 | strong |
Inverse difference moment¶
WF0Z
Inverse difference moment [Haralick1973] is similar in concept to the inverse difference feature, but with lower weights for elements that are further from the diagonal:
The equation above may also be expressed in terms of diagonal probabilities [VanGriethuysen2017]:
This feature is also called homogeneity [Unser1986].
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.619 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.625 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.606 | — | strong |
| dig. phantom | 2.5D, merged | 0.613 | — | strong |
| dig. phantom | 3D, averaged | 0.618 | — | very strong |
| dig. phantom | 3D, merged | 0.631 | — | very strong |
| config. A | 2D, averaged | 0.544 | 0.003 | strong |
| config. A | 2D, slice-merged | 0.544 | 0.003 | strong |
| config. A | 2.5D, direction-merged | 0.573 | 0.003 | strong |
| config. A | 2.5D, merged | 0.573 | 0.003 | strong |
| config. B | 2D, averaged | 0.557 | 0.001 | strong |
| config. B | 2D, slice-merged | 0.558 | 0.001 | strong |
| config. B | 2.5D, direction-merged | 0.6 | 0.001 | strong |
| config. B | 2.5D, merged | 0.6 | 0.001 | strong |
| config. C | 3D, averaged | 0.547 | 0.004 | strong |
| config. C | 3D, merged | 0.548 | 0.004 | very strong |
| config. D | 3D, averaged | 0.656 | 0.003 | strong |
| config. D | 3D, merged | 0.657 | 0.003 | strong |
| config. E | 3D, averaged | 0.576 | 0.001 | strong |
| config. E | 3D, merged | 0.577 | 0.001 | strong |
Normalised inverse difference moment¶
1QCO
[Clausi2002] suggested normalising inverse difference moment to improve classification performance. This leads to the following definition:
The equation above may also be expressed in terms of diagonal probabilities [VanGriethuysen2017]:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.899 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.901 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.897 | — | strong |
| dig. phantom | 2.5D, merged | 0.899 | — | strong |
| dig. phantom | 3D, averaged | 0.898 | — | very strong |
| dig. phantom | 3D, merged | 0.902 | — | very strong |
| config. A | 2D, averaged | 0.994 | 0.001 | strong |
| config. A | 2D, slice-merged | 0.994 | 0.001 | strong |
| config. A | 2.5D, direction-merged | 0.996 | 0.001 | strong |
| config. A | 2.5D, merged | 0.996 | 0.001 | strong |
| config. B | 2D, averaged | 0.99 | 0.001 | strong |
| config. B | 2D, slice-merged | 0.99 | 0.001 | strong |
| config. B | 2.5D, direction-merged | 0.992 | 0.001 | strong |
| config. B | 2.5D, merged | 0.992 | 0.001 | strong |
| config. C | 3D, averaged | 0.994 | 0.001 | strong |
| config. C | 3D, merged | 0.994 | 0.001 | very strong |
| config. D | 3D, averaged | 0.994 | 0.001 | strong |
| config. D | 3D, merged | 0.994 | 0.001 | strong |
| config. E | 3D, averaged | 0.99 | 0.001 | strong |
| config. E | 3D, merged | 0.99 | 0.001 | strong |
Inverse variance¶
E8JP
The inverse variance [Aerts2014] feature is defined as:
The equation above may also be expressed in terms of diagonal probabilities. Note that in this case, summation starts at \(k=1\) instead of \(k=0\)[VanGriethuysen2017]:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.0567 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.0553 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.0597 | — | strong |
| dig. phantom | 2.5D, merged | 0.0582 | — | strong |
| dig. phantom | 3D, averaged | 0.0604 | — | very strong |
| dig. phantom | 3D, merged | 0.0574 | — | very strong |
| config. A | 2D, averaged | 0.441 | 0.001 | strong |
| config. A | 2D, slice-merged | 0.441 | 0.001 | strong |
| config. A | 2.5D, direction-merged | 0.461 | 0.002 | strong |
| config. A | 2.5D, merged | 0.461 | 0.002 | strong |
| config. B | 2D, averaged | 0.401 | 0.002 | strong |
| config. B | 2D, slice-merged | 0.401 | 0.002 | strong |
| config. B | 2.5D, direction-merged | 0.424 | 0.003 | strong |
| config. B | 2.5D, merged | 0.424 | 0.003 | strong |
| config. C | 3D, averaged | 0.39 | 0.003 | strong |
| config. C | 3D, merged | 0.39 | 0.003 | very strong |
| config. D | 3D, averaged | 0.341 | 0.005 | strong |
| config. D | 3D, merged | 0.34 | 0.005 | strong |
| config. E | 3D, averaged | 0.41 | 0.004 | strong |
| config. E | 3D, merged | 0.41 | 0.004 | strong |
Correlation¶
NI2N
Correlation [Haralick1973] is defined as:
\(\mu_{i.}=\sum_{i=1}^{N_g}i\,p_{i.}\) and \(\sigma_{i.}=\left(\sum_{i=1}^{N_g} (i-\mu_{i.})^2 p_{i.}\right)^{1/2}\) are the mean and standard deviation of row marginal probability \(p_{i.}\), respectively. Likewise, \(\mu_{.j}\) and \(\sigma_{.j}\) are the mean and standard deviation of the column marginal probability \(p_{.j}\), respectively. The calculation of correlation can be simplified since \(\mathbf{P}_{\Delta}\) is symmetrical:
An equivalent formulation of correlation is:
Again, simplifying due to matrix symmetry yields:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | \(-\)0.0121 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.0173 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.178 | — | strong |
| dig. phantom | 2.5D, merged | 0.182 | — | strong |
| dig. phantom | 3D, averaged | 0.157 | — | very strong |
| dig. phantom | 3D, merged | 0.183 | — | very strong |
| config. A | 2D, averaged | 0.778 | 0.002 | strong |
| config. A | 2D, slice-merged | 0.78 | 0.002 | strong |
| config. A | 2.5D, direction-merged | 0.839 | 0.003 | strong |
| config. A | 2.5D, merged | 0.84 | 0.003 | strong |
| config. B | 2D, averaged | 0.577 | 0.002 | strong |
| config. B | 2D, slice-merged | 0.58 | 0.002 | strong |
| config. B | 2.5D, direction-merged | 0.693 | 0.003 | strong |
| config. B | 2.5D, merged | 0.695 | 0.003 | strong |
| config. C | 3D, averaged | 0.869 | 0.001 | strong |
| config. C | 3D, merged | 0.871 | 0.001 | strong |
| config. D | 3D, averaged | 0.798 | 0.005 | strong |
| config. D | 3D, merged | 0.8 | 0.005 | strong |
| config. E | 3D, averaged | 0.771 | 0.006 | moderate |
| config. E | 3D, merged | 0.773 | 0.006 | strong |
Autocorrelation¶
QWB0
[soh1999texture] defined autocorrelation as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 5.09 | — | very strong |
| dig. phantom | 2D, slice-merged | 5.14 | — | strong |
| dig. phantom | 2.5D, direction-merged | 5.4 | — | strong |
| dig. phantom | 2.5D, merged | 5.45 | — | strong |
| dig. phantom | 3D, averaged | 5.06 | — | very strong |
| dig. phantom | 3D, merged | 5.19 | — | very strong |
| config. A | 2D, averaged | 455 | 2 | strong |
| config. A | 2D, slice-merged | 455 | 2 | strong |
| config. A | 2.5D, direction-merged | 471 | 2 | strong |
| config. A | 2.5D, merged | 471 | 2 | strong |
| config. B | 2D, averaged | 369 | 11 | strong |
| config. B | 2D, slice-merged | 369 | 11 | strong |
| config. B | 2.5D, direction-merged | 380 | 11 | strong |
| config. B | 2.5D, merged | 380 | 11 | strong |
| config. C | 3D, averaged | \(1.58 \times 10^{3}\) | 10 | strong |
| config. C | 3D, merged | \(1.58 \times 10^{3}\) | 10 | strong |
| config. D | 3D, averaged | 370 | 16 | strong |
| config. D | 3D, merged | 370 | 16 | very strong |
| config. E | 3D, averaged | 509 | 8 | strong |
| config. E | 3D, merged | 509 | 8 | strong |
Cluster tendency¶
DG8W
Cluster tendency [Aerts2014] is defined as:
Here \(\mu_{i.}=\sum_{i=1}^{N_g} i\, p_{i.}\) and \(\mu_{.j}=\sum_{j=1}^{N_g} j\, p_{.j}\). Because of the symmetric nature of \(\mathbf{P}_{\Delta}\), the feature can also be formulated as:
Cluster tendency is mathematically equal to the sum variance feature [VanGriethuysen2017].
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 5.47 | — | very strong |
| dig. phantom | 2D, slice-merged | 5.66 | — | strong |
| dig. phantom | 2.5D, direction-merged | 7.48 | — | strong |
| dig. phantom | 2.5D, merged | 7.65 | — | strong |
| dig. phantom | 3D, averaged | 7.07 | — | very strong |
| dig. phantom | 3D, merged | 7.41 | — | very strong |
| config. A | 2D, averaged | 100 | 1 | strong |
| config. A | 2D, slice-merged | 100 | 1 | strong |
| config. A | 2.5D, direction-merged | 68.5 | 1.3 | strong |
| config. A | 2.5D, merged | 68.5 | 1.3 | strong |
| config. B | 2D, averaged | 72.1 | 1 | strong |
| config. B | 2D, slice-merged | 72.3 | 1 | strong |
| config. B | 2.5D, direction-merged | 48.1 | 0.4 | strong |
| config. B | 2.5D, merged | 48.1 | 0.4 | strong |
| config. C | 3D, averaged | 276 | 8 | strong |
| config. C | 3D, merged | 276 | 8 | very strong |
| config. D | 3D, averaged | 63.4 | 1.3 | strong |
| config. D | 3D, merged | 63.5 | 1.3 | strong |
| config. E | 3D, averaged | 86.6 | 3.3 | moderate |
| config. E | 3D, merged | 86.7 | 3.3 | strong |
Cluster shade¶
7NFM
Cluster shade [Unser1986] is defined as:
As with cluster tendency, \(\mu_{i.}=\sum_{i=1}^{N_g} i\, p_{i.}\) and \(\mu_{.j}=\sum_{j=1}^{N_g} j\, p_{.j}\). Because of the symmetric nature of \(\mathbf{P}_{\Delta}\), the feature can also be formulated as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 7 | — | very strong |
| dig. phantom | 2D, slice-merged | 6.98 | — | strong |
| dig. phantom | 2.5D, direction-merged | 16.6 | — | strong |
| dig. phantom | 2.5D, merged | 16.4 | — | strong |
| dig. phantom | 3D, averaged | 16.6 | — | very strong |
| dig. phantom | 3D, merged | 17.4 | — | very strong |
| config. A | 2D, averaged | \(-1.04 \times 10^{3}\) | 20 | strong |
| config. A | 2D, slice-merged | \(-1.05 \times 10^{3}\) | 20 | strong |
| config. A | 2.5D, direction-merged | \(-1.49 \times 10^{3}\) | 30 | strong |
| config. A | 2.5D, merged | \(-1.49 \times 10^{3}\) | 30 | strong |
| config. B | 2D, averaged | \(-\)668 | 17 | strong |
| config. B | 2D, slice-merged | \(-\)673 | 17 | strong |
| config. B | 2.5D, direction-merged | \(-\)905 | 19 | strong |
| config. B | 2.5D, merged | \(-\)906 | 19 | strong |
| config. C | 3D, averaged | \(-1.06 \times 10^{4}\) | 300 | strong |
| config. C | 3D, merged | \(-1.06 \times 10^{4}\) | 300 | very strong |
| config. D | 3D, averaged | \(-1.27 \times 10^{3}\) | 40 | strong |
| config. D | 3D, merged | \(-1.28 \times 10^{3}\) | 40 | strong |
| config. E | 3D, averaged | \(-2.07 \times 10^{3}\) | 70 | moderate |
| config. E | 3D, merged | \(-2.08 \times 10^{3}\) | 70 | strong |
Cluster prominence¶
AE86
Cluster prominence [Unser1986] is defined as:
As before, \(\mu_{i.}=\sum_{i=1}^{N_g} i\, p_{i.}\) and \(\mu_{.j}=\sum_{j=1}^{N_g} j\, p_{.j}\). Because of the symmetric nature of \(\mathbf{P}_{\Delta}\), the feature can also be formulated as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 79.1 | — | very strong |
| dig. phantom | 2D, slice-merged | 80.4 | — | strong |
| dig. phantom | 2.5D, direction-merged | 147 | — | strong |
| dig. phantom | 2.5D, merged | 142 | — | strong |
| dig. phantom | 3D, averaged | 145 | — | very strong |
| dig. phantom | 3D, merged | 147 | — | very strong |
| config. A | 2D, averaged | \(5.27 \times 10^{4}\) | 500 | strong |
| config. A | 2D, slice-merged | \(5.28 \times 10^{4}\) | 500 | strong |
| config. A | 2.5D, direction-merged | \(4.76 \times 10^{4}\) | 700 | strong |
| config. A | 2.5D, merged | \(4.77 \times 10^{4}\) | 700 | strong |
| config. B | 2D, averaged | \(2.94 \times 10^{4}\) | \(1.4 \times 10^{3}\) | strong |
| config. B | 2D, slice-merged | \(2.95 \times 10^{4}\) | \(1.4 \times 10^{3}\) | strong |
| config. B | 2.5D, direction-merged | \(2.52 \times 10^{4}\) | \(1 \times 10^{3}\) | strong |
| config. B | 2.5D, merged | \(2.53 \times 10^{4}\) | \(1 \times 10^{3}\) | strong |
| config. C | 3D, averaged | \(5.69 \times 10^{5}\) | \(1.1 \times 10^{4}\) | strong |
| config. C | 3D, merged | \(5.7 \times 10^{5}\) | \(1.1 \times 10^{4}\) | very strong |
| config. D | 3D, averaged | \(3.57 \times 10^{4}\) | \(1.4 \times 10^{3}\) | strong |
| config. D | 3D, merged | \(3.57 \times 10^{4}\) | \(1.5 \times 10^{3}\) | very strong |
| config. E | 3D, averaged | \(6.89 \times 10^{4}\) | \(2.1 \times 10^{3}\) | moderate |
| config. E | 3D, merged | \(6.9 \times 10^{4}\) | \(2.1 \times 10^{3}\) | strong |
Information correlation 1¶
R8DG
Information theoretic correlation is estimated using two different measures [Haralick1973]. For symmetric \(\mathbf{P}_{\Delta}\) the first measure is defined as:
\(\mathit{HXY} = -\sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p_{ij} \log_2 p_{ij}\) is the entropy for the joint probability. \(\mathit{HX}=-\sum_{i=1}^{N_g} p_{i.} \log_2 p_{i.}\) is the entropy for the row marginal probability, which due to symmetry is equal to the entropy of the column marginal probability. \(\mathit{HXY}_1\) is a type of entropy that is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | \(-\)0.155 | — | very strong |
| dig. phantom | 2D, slice-merged | \(-\)0.0341 | — | strong |
| dig. phantom | 2.5D, direction-merged | \(-\)0.124 | — | strong |
| dig. phantom | 2.5D, merged | \(-\)0.0334 | — | strong |
| dig. phantom | 3D, averaged | \(-\)0.157 | — | very strong |
| dig. phantom | 3D, merged | \(-\)0.0288 | — | very strong |
| config. A | 2D, averaged | \(-\)0.236 | 0.001 | strong |
| config. A | 2D, slice-merged | \(-\)0.214 | 0.001 | strong |
| config. A | 2.5D, direction-merged | \(-\)0.231 | 0.001 | strong |
| config. A | 2.5D, merged | \(-\)0.228 | 0.001 | strong |
| config. B | 2D, averaged | \(-\)0.239 | 0.001 | strong |
| config. B | 2D, slice-merged | \(-\)0.181 | 0.001 | strong |
| config. B | 2.5D, direction-merged | \(-\)0.188 | 0.001 | strong |
| config. B | 2.5D, merged | \(-\)0.185 | 0.001 | strong |
| config. C | 3D, averaged | \(-\)0.236 | 0.001 | strong |
| config. C | 3D, merged | \(-\)0.228 | 0.001 | very strong |
| config. D | 3D, averaged | \(-\)0.231 | 0.003 | strong |
| config. D | 3D, merged | \(-\)0.225 | 0.003 | strong |
| config. E | 3D, averaged | \(-\)0.181 | 0.003 | moderate |
| config. E | 3D, merged | \(-\)0.175 | 0.003 | strong |
Information correlation 2¶
JN9H
The second measure of information theoretic correlation [Haralick1973] is estimated as follows for symmetric \(\mathbf{P}_{\Delta}\):
As earlier, \(\mathit{HXY} = -\sum_{i=1}^{N_g} \sum_{j=1}^{N_g} p_{ij} \log_2 p_{ij}\). \(\mathit{HXY}_2\) is a type of entropy defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.487 | — | strong |
| dig. phantom | 2D, slice-merged | 0.263 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.487 | — | strong |
| dig. phantom | 2.5D, merged | 0.291 | — | strong |
| dig. phantom | 3D, averaged | 0.52 | — | very strong |
| dig. phantom | 3D, merged | 0.269 | — | very strong |
| config. A | 2D, averaged | 0.863 | 0.003 | strong |
| config. A | 2D, slice-merged | 0.851 | 0.002 | strong |
| config. A | 2.5D, direction-merged | 0.879 | 0.001 | strong |
| config. A | 2.5D, merged | 0.88 | 0.001 | strong |
| config. B | 2D, averaged | 0.837 | 0.001 | strong |
| config. B | 2D, slice-merged | 0.792 | 0.001 | strong |
| config. B | 2.5D, direction-merged | 0.821 | 0.001 | strong |
| config. B | 2.5D, merged | 0.819 | 0.001 | strong |
| config. C | 3D, averaged | 0.9 | 0.001 | strong |
| config. C | 3D, merged | 0.899 | 0.001 | very strong |
| config. D | 3D, averaged | 0.845 | 0.003 | strong |
| config. D | 3D, merged | 0.846 | 0.003 | very strong |
| config. E | 3D, averaged | 0.813 | 0.004 | moderate |
| config. E | 3D, merged | 0.813 | 0.004 | strong |
Grey level run length based features¶
TP0I
The grey level run length matrix (GLRLM) was introduced by [Galloway1975] to define various texture features. Like the grey level co-occurrence matrix, GLRLM also assesses the distribution of discretised grey levels in an image or in a stack of images. However, whereas GLCM assesses co-occurrence of grey levels within neighbouring pixels or voxels, GLRLM assesses run lengths. A run length is defined as the length of a consecutive sequence of pixels or voxels with the same grey level along direction \(\mathbf{m}\), which was previously defined in Grey level co-occurrence based features. The GLRLM then contains the occurrences of runs with length \(j\) for a discretised grey level \(i\).
A complete example for GLRLM construction from a 2D image is shown in Fig. 14. Let \(\mathbf{M}_{\mathbf{m}}\) be the \(N_g \times N_r\) grey level run length matrix, where \(N_g\) is the number of discretised grey levels present in the ROI intensity mask and \(N_r\) the maximal possible run length along direction \(\mathbf{m}\). Matrix element \(r_{ij}\) of the GLRLM is the occurrence of grev level \(i\) with run length \(j\). Then, let \(N_v\) be the total number of voxels in the ROI intensity mask, and \(N_s=\sum_{i=1}^{N_g}\sum_{j=1}^{N_r}r_{ij}\) the sum over all elements in \(\mathbf{M}_{\mathbf{m}}\). Marginal sums are also defined. Let \(r_{i.}\) be the marginal sum of the runs over run lengths \(j\) for grey value \(i\), that is \(r_{i.}=\sum_{j=1}^{N_r} r_{ij}\). Similarly, the marginal sum of the runs over the grey values \(i\) for run length \(j\) is \(r_{.j}=\sum_{i=1}^{N_g} r_{ij}\).

Fig. 14 Grey level run length matrices for the 0◦ (a), 45◦ (b), 90◦ (c) and 135◦ (d) directions. In vector notation these directions are \(\mathbf{m} = (1, 0)\), \(\mathbf{m} = (1, 1)\), \(\mathbf{m} = (0, 1)\) and \(\mathbf{m} = (-1, 1)\), respectively.
Aggregating features¶
To improve rotational invariance, GLRLM feature values are computed by aggregating information from the different underlying directional matrices [Depeursinge2017a]. Five methods can be used to aggregate GLRLMs and arrive at a single feature value. A schematic example was previously shown Fig. 13. A feature may be aggregated as follows:
- Features are computed from each 2D directional matrix and averaged over 2D directions and slices (BTW3).
- Features are computed from a single matrix after merging 2D directional matrices per slice, and then averaged over slices (SUJT).
- Features are computed from a single matrix after merging 2D directional matrices per direction, and then averaged over directions (JJUI).
- The feature is computed from a single matrix after merging all 2D directional matrices (ZW7Z).
- Features are computed from each 3D directional matrix and averaged over the 3D directions (ITBB).
- The feature is computed from a single matrix after merging all 3D directional matrices (IAZD).
In methods 2,3,4 and 6 matrices are merged by summing the run counts of each matrix element \((i,j)\) over the different matrices. Note that when matrices are merged, \(N_v\) should likewise be summed to retain consistency. Feature values may dependent strongly on the aggregation method.
Distance weighting¶
GLRLMs may be weighted for distance by multiplying the run lengths with a weighting factor \(w\). By default \(w=1\), but \(w\) may also be an inverse distance function, e.g. \(w=\|\mathbf{m}\|^{-1}\) or \(w=\exp(-\|\mathbf{m}\|^2)\) [VanGriethuysen2017], with \(\|\mathbf{m}\|\) the length of direction vector \(m\). Whether distance weighting yields different feature values depends on several factors. When aggregating the feature values, matrices have to be merged first, otherwise weighting has no effect. It also has no effect if the Chebyshev norm is used for weighting. Distance weighting is non-standard use, and we caution against it due to potential reproducibility issues.
Short runs emphasis¶
22OV
This feature emphasises short run lengths [Galloway1975]. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.641 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.661 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.665 | — | strong |
| dig. phantom | 2.5D, merged | 0.68 | — | strong |
| dig. phantom | 3D, averaged | 0.705 | — | very strong |
| dig. phantom | 3D, merged | 0.729 | — | very strong |
| config. A | 2D, averaged | 0.785 | 0.003 | strong |
| config. A | 2D, slice-merged | 0.786 | 0.003 | strong |
| config. A | 2.5D, direction-merged | 0.768 | 0.003 | strong |
| config. A | 2.5D, merged | 0.769 | 0.003 | strong |
| config. B | 2D, averaged | 0.781 | 0.001 | strong |
| config. B | 2D, slice-merged | 0.782 | 0.001 | strong |
| config. B | 2.5D, direction-merged | 0.759 | 0.001 | strong |
| config. B | 2.5D, merged | 0.759 | 0.001 | strong |
| config. C | 3D, averaged | 0.786 | 0.003 | strong |
| config. C | 3D, merged | 0.787 | 0.003 | strong |
| config. D | 3D, averaged | 0.734 | 0.001 | strong |
| config. D | 3D, merged | 0.736 | 0.001 | strong |
| config. E | 3D, averaged | 0.776 | 0.001 | moderate |
| config. E | 3D, merged | 0.777 | 0.001 | strong |
Long runs emphasis¶
W4KF
This feature emphasises long run lengths [Galloway1975]. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 3.78 | — | very strong |
| dig. phantom | 2D, slice-merged | 3.51 | — | strong |
| dig. phantom | 2.5D, direction-merged | 3.46 | — | strong |
| dig. phantom | 2.5D, merged | 3.27 | — | strong |
| dig. phantom | 3D, averaged | 3.06 | — | very strong |
| dig. phantom | 3D, merged | 2.76 | — | very strong |
| config. A | 2D, averaged | 2.91 | 0.03 | strong |
| config. A | 2D, slice-merged | 2.89 | 0.03 | strong |
| config. A | 2.5D, direction-merged | 3.09 | 0.03 | strong |
| config. A | 2.5D, merged | 3.08 | 0.03 | strong |
| config. B | 2D, averaged | 3.52 | 0.04 | strong |
| config. B | 2D, slice-merged | 3.5 | 0.04 | strong |
| config. B | 2.5D, direction-merged | 3.82 | 0.05 | strong |
| config. B | 2.5D, merged | 3.81 | 0.05 | strong |
| config. C | 3D, averaged | 3.31 | 0.04 | strong |
| config. C | 3D, merged | 3.28 | 0.04 | strong |
| config. D | 3D, averaged | 6.66 | 0.18 | strong |
| config. D | 3D, merged | 6.56 | 0.18 | strong |
| config. E | 3D, averaged | 3.55 | 0.07 | strong |
| config. E | 3D, merged | 3.52 | 0.07 | strong |
Low grey level run emphasis¶
V3SW
This feature is a grey level analogue to short runs emphasis [Chu1990]. Instead of short run lengths, low grey levels are emphasised. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.604 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.609 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.58 | — | strong |
| dig. phantom | 2.5D, merged | 0.585 | — | strong |
| dig. phantom | 3D, averaged | 0.603 | — | very strong |
| dig. phantom | 3D, merged | 0.607 | — | very strong |
| config. A | 2D, averaged | 0.0264 | 0.0003 | strong |
| config. A | 2D, slice-merged | 0.0264 | 0.0003 | strong |
| config. A | 2.5D, direction-merged | 0.0148 | 0.0004 | strong |
| config. A | 2.5D, merged | 0.0147 | 0.0004 | strong |
| config. B | 2D, averaged | 0.0331 | 0.0006 | strong |
| config. B | 2D, slice-merged | 0.033 | 0.0006 | strong |
| config. B | 2.5D, direction-merged | 0.0194 | 0.0006 | strong |
| config. B | 2.5D, merged | 0.0194 | 0.0006 | strong |
| config. C | 3D, averaged | 0.00155 | \(5 \times 10^{-5}\) | strong |
| config. C | 3D, merged | 0.00155 | \(5 \times 10^{-5}\) | strong |
| config. D | 3D, averaged | 0.0257 | 0.0012 | strong |
| config. D | 3D, merged | 0.0257 | 0.0012 | strong |
| config. E | 3D, averaged | 0.0204 | 0.0008 | moderate |
| config. E | 3D, merged | 0.0204 | 0.0008 | strong |
High grey level run emphasis¶
G3QZ
The high grey level run emphasis feature is a grey level analogue to long runs emphasis [Chu1990]. The feature emphasises high grey levels, and is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 9.82 | — | very strong |
| dig. phantom | 2D, slice-merged | 9.74 | — | strong |
| dig. phantom | 2.5D, direction-merged | 10.3 | — | strong |
| dig. phantom | 2.5D, merged | 10.2 | — | strong |
| dig. phantom | 3D, averaged | 9.7 | — | very strong |
| dig. phantom | 3D, merged | 9.64 | — | very strong |
| config. A | 2D, averaged | 428 | 3 | strong |
| config. A | 2D, slice-merged | 428 | 3 | strong |
| config. A | 2.5D, direction-merged | 449 | 3 | strong |
| config. A | 2.5D, merged | 449 | 3 | strong |
| config. B | 2D, averaged | 342 | 11 | strong |
| config. B | 2D, slice-merged | 342 | 11 | strong |
| config. B | 2.5D, direction-merged | 356 | 11 | strong |
| config. B | 2.5D, merged | 356 | 11 | strong |
| config. C | 3D, averaged | \(1.47 \times 10^{3}\) | 10 | strong |
| config. C | 3D, merged | \(1.47 \times 10^{3}\) | 10 | strong |
| config. D | 3D, averaged | 326 | 17 | strong |
| config. D | 3D, merged | 326 | 17 | strong |
| config. E | 3D, averaged | 471 | 9 | strong |
| config. E | 3D, merged | 471 | 9 | strong |
Short run low grey level emphasis¶
HTZT
This feature emphasises runs in the upper left quadrant of the GLRLM, where short run lengths and low grey levels are located [Dasarathy1991]. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.294 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.311 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.296 | — | strong |
| dig. phantom | 2.5D, merged | 0.312 | — | strong |
| dig. phantom | 3D, averaged | 0.352 | — | very strong |
| dig. phantom | 3D, merged | 0.372 | — | very strong |
| config. A | 2D, averaged | 0.0243 | 0.0003 | strong |
| config. A | 2D, slice-merged | 0.0243 | 0.0003 | strong |
| config. A | 2.5D, direction-merged | 0.0135 | 0.0004 | strong |
| config. A | 2.5D, merged | 0.0135 | 0.0004 | strong |
| config. B | 2D, averaged | 0.0314 | 0.0006 | strong |
| config. B | 2D, slice-merged | 0.0313 | 0.0006 | strong |
| config. B | 2.5D, direction-merged | 0.0181 | 0.0006 | strong |
| config. B | 2.5D, merged | 0.0181 | 0.0006 | strong |
| config. C | 3D, averaged | 0.00136 | \(5 \times 10^{-5}\) | strong |
| config. C | 3D, merged | 0.00136 | \(5 \times 10^{-5}\) | strong |
| config. D | 3D, averaged | 0.0232 | 0.001 | strong |
| config. D | 3D, merged | 0.0232 | 0.001 | strong |
| config. E | 3D, averaged | 0.0187 | 0.0007 | moderate |
| config. E | 3D, merged | 0.0186 | 0.0007 | strong |
Short run high grey level emphasis¶
GD3A
This feature emphasises runs in the lower left quadrant of the GLRLM, where short run lengths and high grey levels are located [Dasarathy1991]. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 8.57 | — | very strong |
| dig. phantom | 2D, slice-merged | 8.67 | — | strong |
| dig. phantom | 2.5D, direction-merged | 9.03 | — | strong |
| dig. phantom | 2.5D, merged | 9.05 | — | strong |
| dig. phantom | 3D, averaged | 8.54 | — | very strong |
| dig. phantom | 3D, merged | 8.67 | — | very strong |
| config. A | 2D, averaged | 320 | 1 | strong |
| config. A | 2D, slice-merged | 320 | 1 | strong |
| config. A | 2.5D, direction-merged | 332 | 1 | strong |
| config. A | 2.5D, merged | 333 | 1 | strong |
| config. B | 2D, averaged | 251 | 8 | strong |
| config. B | 2D, slice-merged | 252 | 8 | strong |
| config. B | 2.5D, direction-merged | 257 | 9 | strong |
| config. B | 2.5D, merged | 258 | 9 | strong |
| config. C | 3D, averaged | \(1.1 \times 10^{3}\) | 10 | strong |
| config. C | 3D, merged | \(1.1 \times 10^{3}\) | 10 | strong |
| config. D | 3D, averaged | 219 | 13 | strong |
| config. D | 3D, merged | 219 | 13 | strong |
| config. E | 3D, averaged | 346 | 7 | strong |
| config. E | 3D, merged | 347 | 7 | strong |
Long run low grey level emphasis¶
IVPO
This feature emphasises runs in the upper right quadrant of the GLRLM, where long run lengths and low grey levels are located [Dasarathy1991]. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 3.14 | — | very strong |
| dig. phantom | 2D, slice-merged | 2.92 | — | strong |
| dig. phantom | 2.5D, direction-merged | 2.79 | — | strong |
| dig. phantom | 2.5D, merged | 2.63 | — | strong |
| dig. phantom | 3D, averaged | 2.39 | — | very strong |
| dig. phantom | 3D, merged | 2.16 | — | very strong |
| config. A | 2D, averaged | 0.0386 | 0.0003 | strong |
| config. A | 2D, slice-merged | 0.0385 | 0.0003 | strong |
| config. A | 2.5D, direction-merged | 0.0229 | 0.0004 | strong |
| config. A | 2.5D, merged | 0.0228 | 0.0004 | strong |
| config. B | 2D, averaged | 0.0443 | 0.0008 | strong |
| config. B | 2D, slice-merged | 0.0442 | 0.0008 | strong |
| config. B | 2.5D, direction-merged | 0.0293 | 0.0009 | strong |
| config. B | 2.5D, merged | 0.0292 | 0.0009 | strong |
| config. C | 3D, averaged | 0.00317 | \(4 \times 10^{-5}\) | strong |
| config. C | 3D, merged | 0.00314 | \(4 \times 10^{-5}\) | strong |
| config. D | 3D, averaged | 0.0484 | 0.0031 | strong |
| config. D | 3D, merged | 0.0478 | 0.0031 | strong |
| config. E | 3D, averaged | 0.0313 | 0.0016 | moderate |
| config. E | 3D, merged | 0.0311 | 0.0016 | strong |
Long run high grey level emphasis¶
3KUM
This feature emphasises runs in the lower right quadrant of the GLRLM, where long run lengths and high grey levels are located [Dasarathy1991]. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 17.4 | — | very strong |
| dig. phantom | 2D, slice-merged | 16.1 | — | strong |
| dig. phantom | 2.5D, direction-merged | 17.9 | — | strong |
| dig. phantom | 2.5D, merged | 17 | — | strong |
| dig. phantom | 3D, averaged | 17.6 | — | very strong |
| dig. phantom | 3D, merged | 15.6 | — | very strong |
| config. A | 2D, averaged | \(1.41 \times 10^{3}\) | 20 | strong |
| config. A | 2D, slice-merged | \(1.4 \times 10^{3}\) | 20 | strong |
| config. A | 2.5D, direction-merged | \(1.5 \times 10^{3}\) | 20 | strong |
| config. A | 2.5D, merged | \(1.5 \times 10^{3}\) | 20 | strong |
| config. B | 2D, averaged | \(1.39 \times 10^{3}\) | 30 | strong |
| config. B | 2D, slice-merged | \(1.38 \times 10^{3}\) | 30 | strong |
| config. B | 2.5D, direction-merged | \(1.5 \times 10^{3}\) | 30 | strong |
| config. B | 2.5D, merged | \(1.5 \times 10^{3}\) | 30 | strong |
| config. C | 3D, averaged | \(5.59 \times 10^{3}\) | 80 | strong |
| config. C | 3D, merged | \(5.53 \times 10^{3}\) | 80 | strong |
| config. D | 3D, averaged | \(2.67 \times 10^{3}\) | 30 | strong |
| config. D | 3D, merged | \(2.63 \times 10^{3}\) | 30 | strong |
| config. E | 3D, averaged | \(1.9 \times 10^{3}\) | 20 | moderate |
| config. E | 3D, merged | \(1.89 \times 10^{3}\) | 20 | strong |
Grey level non-uniformity¶
R5YN
This feature assesses the distribution of runs over the grey values [Galloway1975]. The feature value is low when runs are equally distributed along grey levels. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 5.2 | — | very strong |
| dig. phantom | 2D, slice-merged | 20.5 | — | strong |
| dig. phantom | 2.5D, direction-merged | 19.5 | — | strong |
| dig. phantom | 2.5D, merged | 77.1 | — | strong |
| dig. phantom | 3D, averaged | 21.8 | — | very strong |
| dig. phantom | 3D, merged | 281 | — | very strong |
| config. A | 2D, averaged | 432 | 1 | strong |
| config. A | 2D, slice-merged | \(1.73 \times 10^{3}\) | 10 | strong |
| config. A | 2.5D, direction-merged | \(9.85 \times 10^{3}\) | 10 | strong |
| config. A | 2.5D, merged | \(3.94 \times 10^{4}\) | 100 | strong |
| config. B | 2D, averaged | 107 | 1 | strong |
| config. B | 2D, slice-merged | 427 | 1 | strong |
| config. B | 2.5D, direction-merged | \(2.4 \times 10^{3}\) | 10 | strong |
| config. B | 2.5D, merged | \(9.6 \times 10^{3}\) | 20 | strong |
| config. C | 3D, averaged | \(3.18 \times 10^{3}\) | 10 | strong |
| config. C | 3D, merged | \(4.13 \times 10^{4}\) | 100 | strong |
| config. D | 3D, averaged | \(3.29 \times 10^{3}\) | 10 | strong |
| config. D | 3D, merged | \(4.28 \times 10^{4}\) | 200 | strong |
| config. E | 3D, averaged | \(4 \times 10^{3}\) | 10 | moderate |
| config. E | 3D, merged | \(5.19 \times 10^{4}\) | 200 | strong |
Normalised grey level non-uniformity¶
OVBL
This is a normalised version of the grey level non-uniformity feature. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.46 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.456 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.413 | — | strong |
| dig. phantom | 2.5D, merged | 0.412 | — | strong |
| dig. phantom | 3D, averaged | 0.43 | — | very strong |
| dig. phantom | 3D, merged | 0.43 | — | very strong |
| config. A | 2D, averaged | 0.128 | 0.003 | strong |
| config. A | 2D, slice-merged | 0.128 | 0.003 | strong |
| config. A | 2.5D, direction-merged | 0.126 | 0.003 | strong |
| config. A | 2.5D, merged | 0.126 | 0.003 | strong |
| config. B | 2D, averaged | 0.145 | 0.001 | strong |
| config. B | 2D, slice-merged | 0.145 | 0.001 | strong |
| config. B | 2.5D, direction-merged | 0.137 | 0.001 | strong |
| config. B | 2.5D, merged | 0.137 | 0.001 | strong |
| config. C | 3D, averaged | 0.102 | 0.003 | strong |
| config. C | 3D, merged | 0.102 | 0.003 | very strong |
| config. D | 3D, averaged | 0.133 | 0.002 | strong |
| config. D | 3D, merged | 0.134 | 0.002 | strong |
| config. E | 3D, averaged | 0.135 | 0.003 | strong |
| config. E | 3D, merged | 0.135 | 0.003 | strong |
Run length non-uniformity¶
W92Y
This features assesses the distribution of runs over the run lengths [Galloway1975]. The feature value is low when runs are equally distributed along run lengths. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 6.12 | — | very strong |
| dig. phantom | 2D, slice-merged | 21.6 | — | strong |
| dig. phantom | 2.5D, direction-merged | 22.3 | — | strong |
| dig. phantom | 2.5D, merged | 83.2 | — | strong |
| dig. phantom | 3D, averaged | 26.9 | — | very strong |
| dig. phantom | 3D, merged | 328 | — | very strong |
| config. A | 2D, averaged | \(1.65 \times 10^{3}\) | 10 | strong |
| config. A | 2D, slice-merged | \(6.6 \times 10^{3}\) | 30 | strong |
| config. A | 2.5D, direction-merged | \(4.27 \times 10^{4}\) | 200 | strong |
| config. A | 2.5D, merged | \(1.71 \times 10^{5}\) | \(1 \times 10^{3}\) | strong |
| config. B | 2D, averaged | 365 | 3 | strong |
| config. B | 2D, slice-merged | \(1.46 \times 10^{3}\) | 10 | strong |
| config. B | 2.5D, direction-merged | \(9.38 \times 10^{3}\) | 70 | strong |
| config. B | 2.5D, merged | \(3.75 \times 10^{4}\) | 300 | strong |
| config. C | 3D, averaged | \(1.8 \times 10^{4}\) | 500 | strong |
| config. C | 3D, merged | \(2.34 \times 10^{5}\) | \(6 \times 10^{3}\) | strong |
| config. D | 3D, averaged | \(1.24 \times 10^{4}\) | 200 | strong |
| config. D | 3D, merged | \(1.6 \times 10^{5}\) | \(3 \times 10^{3}\) | strong |
| config. E | 3D, averaged | \(1.66 \times 10^{4}\) | 300 | strong |
| config. E | 3D, merged | \(2.15 \times 10^{5}\) | \(4 \times 10^{3}\) | strong |
Normalised run length non-uniformity¶
IC23
This is normalised version of the run length non-uniformity feature. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.492 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.441 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.461 | — | strong |
| dig. phantom | 2.5D, merged | 0.445 | — | strong |
| dig. phantom | 3D, averaged | 0.513 | — | very strong |
| dig. phantom | 3D, merged | 0.501 | — | very strong |
| config. A | 2D, averaged | 0.579 | 0.003 | strong |
| config. A | 2D, slice-merged | 0.579 | 0.003 | strong |
| config. A | 2.5D, direction-merged | 0.548 | 0.003 | strong |
| config. A | 2.5D, merged | 0.548 | 0.003 | strong |
| config. B | 2D, averaged | 0.578 | 0.001 | strong |
| config. B | 2D, slice-merged | 0.578 | 0.001 | strong |
| config. B | 2.5D, direction-merged | 0.533 | 0.001 | strong |
| config. B | 2.5D, merged | 0.534 | 0.001 | strong |
| config. C | 3D, averaged | 0.574 | 0.004 | strong |
| config. C | 3D, merged | 0.575 | 0.004 | strong |
| config. D | 3D, averaged | 0.5 | 0.001 | strong |
| config. D | 3D, merged | 0.501 | 0.001 | strong |
| config. E | 3D, averaged | 0.559 | 0.001 | moderate |
| config. E | 3D, merged | 0.56 | 0.001 | strong |
Run percentage¶
9ZK5
This feature measures the fraction of the number of realised runs and the maximum number of potential runs [Galloway1975]. Strongly linear or highly uniform ROI volumes produce a low run percentage. It is defined as:
As noted before, when this feature is calculated using a merged GLRLM, \(N_v\) should be the sum of the number of voxels of the underlying matrices to allow proper normalisation.
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.627 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.627 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.632 | — | strong |
| dig. phantom | 2.5D, merged | 0.632 | — | strong |
| dig. phantom | 3D, averaged | 0.68 | — | very strong |
| dig. phantom | 3D, merged | 0.68 | — | very strong |
| config. A | 2D, averaged | 0.704 | 0.003 | strong |
| config. A | 2D, slice-merged | 0.704 | 0.003 | strong |
| config. A | 2.5D, direction-merged | 0.68 | 0.003 | strong |
| config. A | 2.5D, merged | 0.68 | 0.003 | strong |
| config. B | 2D, averaged | 0.681 | 0.002 | strong |
| config. B | 2D, slice-merged | 0.681 | 0.002 | strong |
| config. B | 2.5D, direction-merged | 0.642 | 0.002 | strong |
| config. B | 2.5D, merged | 0.642 | 0.002 | strong |
| config. C | 3D, averaged | 0.679 | 0.003 | strong |
| config. C | 3D, merged | 0.679 | 0.003 | strong |
| config. D | 3D, averaged | 0.554 | 0.005 | strong |
| config. D | 3D, merged | 0.554 | 0.005 | strong |
| config. E | 3D, averaged | 0.664 | 0.003 | moderate |
| config. E | 3D, merged | 0.664 | 0.003 | strong |
Grey level variance¶
8CE5
This feature estimates the variance in runs over the grey levels. Let \(p_{ij} = r_{ij}/N_s\) be the joint probability estimate for finding discretised grey level \(i\) with run length \(j\). Grey level variance is then defined as:
Here, \(\mu = \sum_{i=1}^{N_g} \sum_{j=1}^{N_r} i\,p_{ij}\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 3.35 | — | very strong |
| dig. phantom | 2D, slice-merged | 3.37 | — | strong |
| dig. phantom | 2.5D, direction-merged | 3.58 | — | strong |
| dig. phantom | 2.5D, merged | 3.59 | — | strong |
| dig. phantom | 3D, averaged | 3.46 | — | very strong |
| dig. phantom | 3D, merged | 3.48 | — | very strong |
| config. A | 2D, averaged | 33.7 | 0.6 | strong |
| config. A | 2D, slice-merged | 33.7 | 0.6 | strong |
| config. A | 2.5D, direction-merged | 29.1 | 0.6 | strong |
| config. A | 2.5D, merged | 29.1 | 0.6 | strong |
| config. B | 2D, averaged | 28.3 | 0.3 | strong |
| config. B | 2D, slice-merged | 28.3 | 0.3 | strong |
| config. B | 2.5D, direction-merged | 25.7 | 0.2 | strong |
| config. B | 2.5D, merged | 25.7 | 0.2 | strong |
| config. C | 3D, averaged | 101 | 3 | strong |
| config. C | 3D, merged | 101 | 3 | very strong |
| config. D | 3D, averaged | 31.5 | 0.4 | strong |
| config. D | 3D, merged | 31.4 | 0.4 | strong |
| config. E | 3D, averaged | 39.8 | 0.9 | moderate |
| config. E | 3D, merged | 39.7 | 0.9 | strong |
Run length variance¶
SXLW
This feature estimates the variance in runs over the run lengths. As before let \(p_{ij} = r_{ij}/N_s\). The feature is defined as:
Mean run length is defined as \(\mu = \sum_{i=1}^{N_g} \sum_{j=1}^{N_r} j\,p_{ij}\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 0.761 | — | very strong |
| dig. phantom | 2D, slice-merged | 0.778 | — | strong |
| dig. phantom | 2.5D, direction-merged | 0.758 | — | strong |
| dig. phantom | 2.5D, merged | 0.767 | — | strong |
| dig. phantom | 3D, averaged | 0.574 | — | very strong |
| dig. phantom | 3D, merged | 0.598 | — | very strong |
| config. A | 2D, averaged | 0.828 | 0.008 | strong |
| config. A | 2D, slice-merged | 0.826 | 0.008 | strong |
| config. A | 2.5D, direction-merged | 0.916 | 0.011 | strong |
| config. A | 2.5D, merged | 0.914 | 0.011 | strong |
| config. B | 2D, averaged | 1.22 | 0.03 | strong |
| config. B | 2D, slice-merged | 1.21 | 0.03 | strong |
| config. B | 2.5D, direction-merged | 1.39 | 0.03 | strong |
| config. B | 2.5D, merged | 1.39 | 0.03 | strong |
| config. C | 3D, averaged | 1.12 | 0.02 | strong |
| config. C | 3D, merged | 1.11 | 0.02 | strong |
| config. D | 3D, averaged | 3.35 | 0.14 | strong |
| config. D | 3D, merged | 3.29 | 0.13 | strong |
| config. E | 3D, averaged | 1.26 | 0.05 | strong |
| config. E | 3D, merged | 1.25 | 0.05 | strong |
Run entropy¶
HJ9O
Run entropy was investigated by [Albregtsen2000]. Again, let \(p_{ij} = r_{ij}/N_s\). The entropy is then defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D, averaged | 2.17 | — | very strong |
| dig. phantom | 2D, slice-merged | 2.57 | — | strong |
| dig. phantom | 2.5D, direction-merged | 2.52 | — | strong |
| dig. phantom | 2.5D, merged | 2.76 | — | strong |
| dig. phantom | 3D, averaged | 2.43 | — | very strong |
| dig. phantom | 3D, merged | 2.62 | — | very strong |
| config. A | 2D, averaged | 4.73 | 0.02 | strong |
| config. A | 2D, slice-merged | 4.76 | 0.02 | strong |
| config. A | 2.5D, direction-merged | 4.87 | 0.01 | strong |
| config. A | 2.5D, merged | 4.87 | 0.01 | strong |
| config. B | 2D, averaged | 4.53 | 0.02 | strong |
| config. B | 2D, slice-merged | 4.58 | 0.01 | strong |
| config. B | 2.5D, direction-merged | 4.84 | 0.01 | strong |
| config. B | 2.5D, merged | 4.84 | 0.01 | strong |
| config. C | 3D, averaged | 5.35 | 0.03 | strong |
| config. C | 3D, merged | 5.35 | 0.03 | very strong |
| config. D | 3D, averaged | 5.08 | 0.02 | strong |
| config. D | 3D, merged | 5.08 | 0.02 | very strong |
| config. E | 3D, averaged | 4.87 | 0.03 | strong |
| config. E | 3D, merged | 4.87 | 0.03 | strong |
Grey level size zone based features¶
9SAK
The grey level size zone matrix (GLSZM) counts the number of groups (or zones) of linked voxels [Thibault2014]. Voxels are linked if the neighbouring voxel has an identical discretised grey level. Whether a voxel classifies as a neighbour depends on its connectedness. In a 3D approach to texture analysis we consider 26-connectedness, which indicates that a center voxel is linked to all of the 26 neighbouring voxels with the same grey level. In the 2 dimensional approach, 8-connectedness is used. A potential issue for the 2D approach is that voxels which may otherwise be considered to belong to the same zone by linking across slices, are now two or more separate zones within the slice plane. Whether this issue negatively affects predictive performance of GLSZM-based features or their reproducibility has not been determined.
Let \(\mathbf{M}\) be the \(N_g \times N_z\) grey level size zone matrix, where \(N_g\) is the number of discretised grey levels present in the ROI intensity mask and \(N_z\) the maximum zone size of any group of linked voxels. Element \(s_{ij}\) of \(\mathbf{M}\) is then the number of zones with discretised grey level \(i\) and size \(j\). Furthermore, let \(N_v\) be the number of voxels in the intensity mask and \(N_s=\sum_{i=1}^{N_g}\sum_{j=1}^{N_z}s_{ij}\) be the total number of zones. Marginal sums can likewise be defined. Let \(s_{i.}=\sum_{j=1}^{N_z}s_{ij}\) be the number of zones with discretised grey level \(i\), regardless of size. Likewise, let \(s_{.j}=\sum_{i=1}^{N_g}s_{ij}\) be the number of zones with size \(j\), regardless of grey level. A two dimensional example is shown in Fig. 15.
Fig. 15 Original image with grey levels (a); and corresponding grey level size zone matrix (GLSZM) under 8-connectedness (b). Element \(s_{i,j}\) of the GLSZM indicates the number of times a zone of \(j\) linked pixels and grey level \(i\) occurs within the image.
Aggregating features¶
Three methods can be used to aggregate GLSZMs and arrive at a single feature value. A schematic example is shown in Fig. 16. A feature may be aggregated as follows:
- Features are computed from 2D matrices and averaged over slices (8QNN).
- The feature is computed from a single matrix after merging all 2D matrices (62GR).
- The feature is computed from a 3D matrix (KOBO).
Method 2 involves merging GLSZMs by summing the number of zones \(s_{ij}\) over the GLSZM for the different slices. Note that when matrices are merged, \(N_v\) should likewise be summed to retain consistency. Feature values may dependent strongly on the aggregation method.
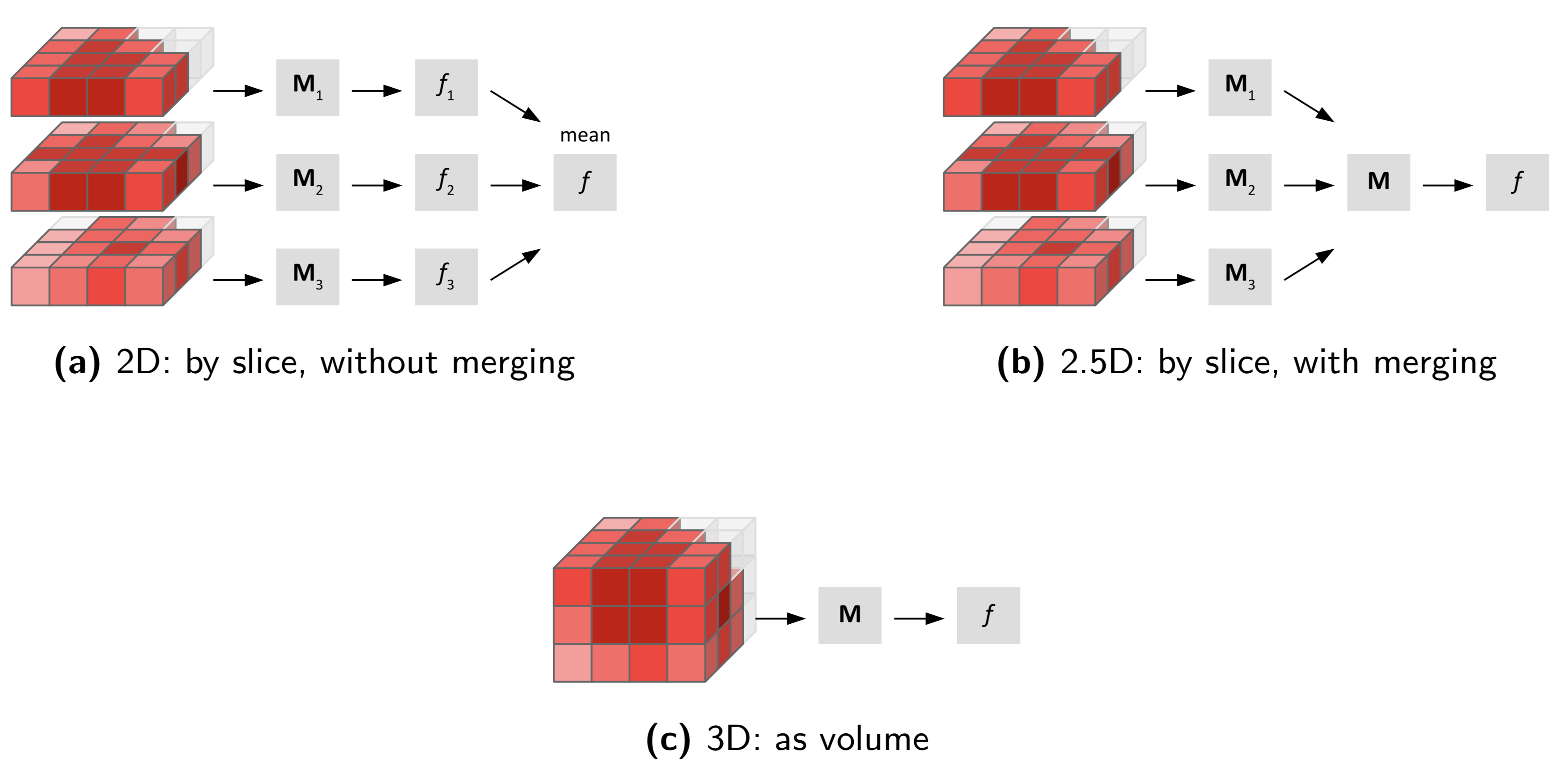
Fig. 16 Approaches to calculating grey level size zone matrix-based features. \(\mathbf{M}_{k}\) are texture matrices calculated for slice \(k\) (if applicable), and \(f_{k}\) is the corresponding feature value. In (b) the matrices from the different slices are merged prior to feature calculation.
Distances¶
The default neighbourhood for GLSZM is constructed using Chebyshev distance \(\delta=1\). Manhattan or Euclidean norms may also be used to construct a neighbourhood, and both lead to a 6-connected (3D) and 4-connected (2D) neighbourhoods. Larger distances are also technically possible, but will occasionally cause separate zones with the same intensity to be considered as belonging to the same zone. Using different neighbourhoods for determining voxel linkage is non-standard use, and we caution against it due to potential reproducibility issues.
Note on feature references¶
GLSZM feature definitions are based on the definitions of GLRLM features [Thibault2014]. Hence, references may be found in the section on GLRLM (Grey level run length based features).
Small zone emphasis¶
This feature emphasises small zones. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.363 | — | strong |
| dig. phantom | 2.5D | 0.368 | — | strong |
| dig. phantom | 3D | 0.255 | — | very strong |
| config. A | 2D | 0.688 | 0.003 | strong |
| config. A | 2.5D | 0.68 | 0.003 | strong |
| config. B | 2D | 0.745 | 0.003 | strong |
| config. B | 2.5D | 0.741 | 0.003 | strong |
| config. C | 3D | 0.695 | 0.001 | strong |
| config. D | 3D | 0.637 | 0.005 | strong |
| config. E | 3D | 0.676 | 0.003 | strong |
Large zone emphasis¶
48P8
This feature emphasises large zones. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 43.9 | — | strong |
| dig. phantom | 2.5D | 34.2 | — | strong |
| dig. phantom | 3D | 550 | — | very strong |
| config. A | 2D | 625 | 9 | strong |
| config. A | 2.5D | 675 | 8 | strong |
| config. B | 2D | 439 | 8 | strong |
| config. B | 2.5D | 444 | 8 | strong |
| config. C | 3D | \(3.89 \times 10^{4}\) | 900 | strong |
| config. D | 3D | \(9.91 \times 10^{4}\) | \(2.8 \times 10^{3}\) | strong |
| config. E | 3D | \(5.86 \times 10^{4}\) | 800 | strong |
Low grey level zone emphasis¶
XMSY
This feature is a grey level analogue to small zone emphasis. Instead of small zone sizes, low grey levels are emphasised. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.371 | — | strong |
| dig. phantom | 2.5D | 0.368 | — | strong |
| dig. phantom | 3D | 0.253 | — | very strong |
| config. A | 2D | 0.0368 | 0.0005 | strong |
| config. A | 2.5D | 0.0291 | 0.0005 | strong |
| config. B | 2D | 0.0475 | 0.001 | strong |
| config. B | 2.5D | 0.0387 | 0.001 | strong |
| config. C | 3D | 0.00235 | \(6 \times 10^{-5}\) | strong |
| config. D | 3D | 0.0409 | 0.0005 | strong |
| config. E | 3D | 0.034 | 0.0004 | strong |
High grey level zone emphasis¶
5GN9
The high grey level zone emphasis feature is a grey level analogue to large zone emphasis. The feature emphasises high grey levels, and is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 16.4 | — | strong |
| dig. phantom | 2.5D | 16.2 | — | strong |
| dig. phantom | 3D | 15.6 | — | very strong |
| config. A | 2D | 363 | 3 | strong |
| config. A | 2.5D | 370 | 3 | strong |
| config. B | 2D | 284 | 11 | strong |
| config. B | 2.5D | 284 | 11 | strong |
| config. C | 3D | 971 | 7 | strong |
| config. D | 3D | 188 | 10 | strong |
| config. E | 3D | 286 | 6 | strong |
Small zone low grey level emphasis¶
5RAI
This feature emphasises zone counts within the upper left quadrant of the GLSZM, where small zone sizes and low grey levels are located. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.0259 | — | strong |
| dig. phantom | 2.5D | 0.0295 | — | strong |
| dig. phantom | 3D | 0.0256 | — | very strong |
| config. A | 2D | 0.0298 | 0.0005 | strong |
| config. A | 2.5D | 0.0237 | 0.0005 | strong |
| config. B | 2D | 0.0415 | 0.0008 | strong |
| config. B | 2.5D | 0.0335 | 0.0009 | strong |
| config. C | 3D | 0.0016 | \(4 \times 10^{-5}\) | strong |
| config. D | 3D | 0.0248 | 0.0004 | strong |
| config. E | 3D | 0.0224 | 0.0004 | strong |
Small zone high grey level emphasis¶
HW1V
This feature emphasises zone counts in the lower left quadrant of the GLSZM, where small zone sizes and high grey levels are located. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 10.3 | — | strong |
| dig. phantom | 2.5D | 9.87 | — | strong |
| dig. phantom | 3D | 2.76 | — | very strong |
| config. A | 2D | 226 | 1 | strong |
| config. A | 2.5D | 229 | 1 | strong |
| config. B | 2D | 190 | 7 | strong |
| config. B | 2.5D | 190 | 7 | strong |
| config. C | 3D | 657 | 4 | strong |
| config. D | 3D | 117 | 7 | strong |
| config. E | 3D | 186 | 4 | strong |
Large zone low grey level emphasis¶
YH51
This feature emphasises zone counts in the upper right quadrant of the GLSZM, where large zone sizes and low grey levels are located. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 40.4 | — | strong |
| dig. phantom | 2.5D | 30.6 | — | strong |
| dig. phantom | 3D | 503 | — | very strong |
| config. A | 2D | 1.35 | 0.03 | strong |
| config. A | 2.5D | 1.44 | 0.02 | strong |
| config. B | 2D | 1.15 | 0.04 | strong |
| config. B | 2.5D | 1.16 | 0.04 | strong |
| config. C | 3D | 21.6 | 0.5 | strong |
| config. D | 3D | 241 | 14 | strong |
| config. E | 3D | 105 | 4 | strong |
Large zone high grey level emphasis¶
J17V
This feature emphasises zone counts in the lower right quadrant of the GLSZM, where large zone sizes and high grey levels are located. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 113 | — | strong |
| dig. phantom | 2.5D | 107 | — | strong |
| dig. phantom | 3D | \(1.49 \times 10^{3}\) | — | very strong |
| config. A | 2D | \(3.16 \times 10^{5}\) | \(5 \times 10^{3}\) | strong |
| config. A | 2.5D | \(3.38 \times 10^{5}\) | \(5 \times 10^{3}\) | strong |
| config. B | 2D | \(1.81 \times 10^{5}\) | \(3 \times 10^{3}\) | strong |
| config. B | 2.5D | \(1.81 \times 10^{5}\) | \(3 \times 10^{3}\) | strong |
| config. C | 3D | \(7.07 \times 10^{7}\) | \(1.5 \times 10^{6}\) | strong |
| config. D | 3D | \(4.14 \times 10^{7}\) | \(3 \times 10^{5}\) | strong |
| config. E | 3D | \(3.36 \times 10^{7}\) | \(3 \times 10^{5}\) | strong |
Grey level non-uniformity¶
JNSA
This feature assesses the distribution of zone counts over the grey values. The feature value is low when zone counts are equally distributed along grey levels. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 1.41 | — | strong |
| dig. phantom | 2.5D | 5.44 | — | strong |
| dig. phantom | 3D | 1.4 | — | very strong |
| config. A | 2D | 82.2 | 0.1 | strong |
| config. A | 2.5D | \(1.8 \times 10^{3}\) | 10 | strong |
| config. B | 2D | 20.5 | 0.1 | strong |
| config. B | 2.5D | 437 | 3 | strong |
| config. C | 3D | 195 | 6 | strong |
| config. D | 3D | 212 | 6 | very strong |
| config. E | 3D | 231 | 6 | strong |
Normalised grey level non-uniformity¶
Y1RO
This is a normalised version of the grey level non-uniformity feature. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.323 | — | strong |
| dig. phantom | 2.5D | 0.302 | — | strong |
| dig. phantom | 3D | 0.28 | — | very strong |
| config. A | 2D | 0.0728 | 0.0014 | strong |
| config. A | 2.5D | 0.0622 | 0.0007 | strong |
| config. B | 2D | 0.0789 | 0.001 | strong |
| config. B | 2.5D | 0.0613 | 0.0005 | strong |
| config. C | 3D | 0.0286 | 0.0003 | strong |
| config. D | 3D | 0.0491 | 0.0008 | strong |
| config. E | 3D | 0.0414 | 0.0003 | strong |
Zone size non-uniformity¶
4JP3
This features assesses the distribution of zone counts over the different zone sizes. Zone size non-uniformity is low when zone counts are equally distributed along zone sizes. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 1.49 | — | strong |
| dig. phantom | 2.5D | 3.44 | — | strong |
| dig. phantom | 3D | 1 | — | very strong |
| config. A | 2D | 479 | 4 | strong |
| config. A | 2.5D | \(1.24 \times 10^{4}\) | 100 | strong |
| config. B | 2D | 140 | 3 | strong |
| config. B | 2.5D | \(3.63 \times 10^{3}\) | 70 | strong |
| config. C | 3D | \(3.04 \times 10^{3}\) | 100 | strong |
| config. D | 3D | \(1.63 \times 10^{3}\) | 10 | strong |
| config. E | 3D | \(2.37 \times 10^{3}\) | 40 | strong |
Normalised zone size non-uniformity¶
VB3A
This is a normalised version of zone size non-uniformity. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.333 | — | strong |
| dig. phantom | 2.5D | 0.191 | — | strong |
| dig. phantom | 3D | 0.2 | — | very strong |
| config. A | 2D | 0.44 | 0.004 | strong |
| config. A | 2.5D | 0.427 | 0.004 | strong |
| config. B | 2D | 0.521 | 0.004 | strong |
| config. B | 2.5D | 0.509 | 0.004 | strong |
| config. C | 3D | 0.447 | 0.001 | strong |
| config. D | 3D | 0.377 | 0.006 | strong |
| config. E | 3D | 0.424 | 0.004 | strong |
Zone percentage¶
P30P
This feature measures the fraction of the number of realised zones and the maximum number of potential zones. Highly uniform ROIs produce a low zone percentage. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.24 | — | strong |
| dig. phantom | 2.5D | 0.243 | — | strong |
| dig. phantom | 3D | 0.0676 | — | very strong |
| config. A | 2D | 0.3 | 0.003 | strong |
| config. A | 2.5D | 0.253 | 0.004 | strong |
| config. B | 2D | 0.324 | 0.001 | strong |
| config. B | 2.5D | 0.26 | 0.002 | strong |
| config. C | 3D | 0.148 | 0.003 | strong |
| config. D | 3D | 0.0972 | 0.0007 | strong |
| config. E | 3D | 0.126 | 0.001 | strong |
Grey level variance¶
BYLV
This feature estimates the variance in zone counts over the grey levels. Let \(p_{ij} = s_{ij}/N_s\) be the joint probability estimate for finding zones with discretised grey level \(i\) and size \(j\). The feature is then defined as:
Here, \(\mu = \sum_{i=1}^{N_g} \sum_{j=1}^{N_z} i\,p_{ij}\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 3.97 | — | strong |
| dig. phantom | 2.5D | 3.92 | — | strong |
| dig. phantom | 3D | 2.64 | — | very strong |
| config. A | 2D | 42.7 | 0.7 | strong |
| config. A | 2.5D | 47.9 | 0.4 | strong |
| config. B | 2D | 36.1 | 0.3 | strong |
| config. B | 2.5D | 41 | 0.7 | strong |
| config. C | 3D | 106 | 1 | strong |
| config. D | 3D | 32.7 | 1.6 | strong |
| config. E | 3D | 50.8 | 0.9 | strong |
Zone size variance¶
3NSA
This feature estimates the variance in zone counts over the different zone sizes. As before let \(p_{ij} = s_{ij}/N_s\). The feature is defined as:
Mean zone size is defined as \(\mu = \sum_{i=1}^{N_g} \sum_{j=1}^{N_z} j\,p_{ij}\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 21 | — | strong |
| dig. phantom | 2.5D | 17.3 | — | strong |
| dig. phantom | 3D | 331 | — | very strong |
| config. A | 2D | 609 | 9 | strong |
| config. A | 2.5D | 660 | 8 | strong |
| config. B | 2D | 423 | 8 | strong |
| config. B | 2.5D | 429 | 8 | strong |
| config. C | 3D | \(3.89 \times 10^{4}\) | 900 | strong |
| config. D | 3D | \(9.9 \times 10^{4}\) | \(2.8 \times 10^{3}\) | strong |
| config. E | 3D | \(5.85 \times 10^{4}\) | 800 | strong |
Zone size entropy¶
GU8N
Let \(p_{ij} = s_{ij}/N_s\). Zone size entropy is then defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 1.93 | — | strong |
| dig. phantom | 2.5D | 3.08 | — | strong |
| dig. phantom | 3D | 2.32 | — | very strong |
| config. A | 2D | 5.92 | 0.02 | strong |
| config. A | 2.5D | 6.39 | 0.01 | strong |
| config. B | 2D | 5.29 | 0.01 | strong |
| config. B | 2.5D | 5.98 | 0.02 | strong |
| config. C | 3D | 7 | 0.01 | strong |
| config. D | 3D | 6.52 | 0.01 | strong |
| config. E | 3D | 6.57 | 0.01 | strong |
Grey level distance zone based features¶
VMDZ
The grey level distance zone matrix (GLDZM) counts the number of groups (or zones) of linked voxels which share a specific discretised grey level value and possess the same distance to ROI edge [Thibault2014]. The GLDZM thus captures the relation between location and grey level. Two maps are required to calculate the GLDZM. The first is a grey level zone map, which is identical to the one created for the grey level size zone matrix (GLSZM), see Grey level size zone based features. The second is a distance map, which will be described in detail later.
As with GSLZM, neighbouring voxels are linked if they share the same grey level value. Whether a voxel classifies as a neighbour depends on its connectedness. We consider 26-connectedness for a 3D approach and 8-connectedness in the 2D approach.
The distance to the ROI edge is defined according to 6 and 4-connectedness for 3D and 2D, respectively. Because of the connectedness definition used, the distance of a voxel to the outer border is equal to the minimum number edges of neighbouring voxels that need to be crossed to reach the ROI edge. The distance for a linked group of voxels with the same grey value is equal to the minimum distance for the respective voxels in the distance map.
Our definition deviates from the original by [Thibault2014]. The original was defined in a rectangular 2D image, whereas ROIs are rarely rectangular cuboids. Approximating distance using Chamfer maps is then no longer a fast and easy solution. Determining distance iteratively in 6 or 4-connectedness is a relatively efficient solution, implemented as follows:
- The ROI mask is morphologically eroded using the appropriate (6 or 4-connected) structure element.
- All eroded ROI voxels are updated in the distance map by adding 1.
- The above steps are performed iteratively until the ROI mask is empty.
A second difference with the original definition is that the lowest possible distance is \(1\) instead of \(0\) for voxels directly on the ROI edge. This prevents division by \(0\) for some features.
Let \(\mathbf{M}\) be the \(N_g \times N_d\) grey level size zone matrix, where \(N_g\) is the number of discretised grey levels present in the ROI intensity mask and \(N_d\) the largest distance of any zone. Element \(d_{ij}=d(i,j)\) of \(\mathbf{M}\) is then number of zones with discretised grey level \(i\) and distance \(j\). Furthermore, let \(N_v\) be the number of voxels and \(N_s=\sum_{i=1}^{N_g}\sum_{j=1}^{N_d}d_{ij}\) be the total zone count. Marginal sums can likewise be defined. Let \(d_{i.}=\sum_{j=1}^{N_d}d_{ij}\) be the number of zones with discretised grey level \(i\), regardless of distance. Likewise, let \(d_{.j}=\sum_{i=1}^{N_g}d_{ij}\) be the number of zones with distance \(j\), regardless of grey level. A two dimensional example is shown in Fig. 17.

Fig. 17 Original image with grey levels (a); corresponding distance map for distance to border (b); and corresponding grey level distance zone matrix (GLDZM) under 4-connectedness (c). Element \(d_{i,j}\) of the GLDZM indicates the number of times a zone with grey level \(i\) and a minimum distance to border \(j\) occurs within the image.
Morphological and intensity masks.¶
The GLDZM is special in that it uses both ROI masks. The distance map is determined using the morphological ROI mask, whereas the intensity mask is used for determining the zones, as with the GLSZM.
Aggregating features¶
Three methods can be used to aggregate GLDZMs and arrive at a single feature value. A schematic example was previously shown in Figure Fig. 16. A feature may be aggregated as follows:
- Features are computed from 2D matrices and averaged over slices (8QNN).
- The feature is computed from a single matrix after merging all 2D matrices (62GR).
- The feature is computed from a 3D matrix (KOBO).
Method 2 involves merging GLDZMs by summing the number of zones \(d_{ij}\) over the GLDZM for the different slices. Note that when matrices are merged, \(N_v\) should likewise be summed to retain consistency. Feature values may dependent strongly on the aggregation method.
Distances¶
In addition to the use of different distance norms to determine voxel linkage, as described in Grey level size zone based features, different distance norms may be used to determine distance of zones to the boundary. The default is to use the Manhattan norm which allows for a computationally efficient implementation, as described above. A similar implementation is possible using the Chebyshev norm, as it merely changes connectedness of the structure element. Implementations using an Euclidean distance norm are less efficient as this demands searching for the nearest non-ROI voxel for each of the \(N_v\) voxels in the ROI. An added issue is that Euclidean norms may lead to a wide range of different distances \(j\) that require rounding before constructing the grey level distance zone matrix \(\mathbf{M}\). Using different distance norms is non-standard use, and we caution against it due to potential reproducibility issues.
Note on feature references¶
GLDZM feature definitions are based on the definitions of GLRLM features [Thibault2014]. Hence, references may be found in the section on GLRLM (Grey level run length based features).
Small distance emphasis¶
0GBI
This feature emphasises small distances. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.946 | — | strong |
| dig. phantom | 2.5D | 0.917 | — | moderate |
| dig. phantom | 3D | 1 | — | very strong |
| config. A | 2D | 0.192 | 0.006 | strong |
| config. A | 2.5D | 0.168 | 0.005 | strong |
| config. B | 2D | 0.36 | 0.005 | strong |
| config. B | 2.5D | 0.329 | 0.004 | strong |
| config. C | 3D | 0.531 | 0.006 | strong |
| config. D | 3D | 0.579 | 0.004 | strong |
| config. E | 3D | 0.527 | 0.004 | moderate |
Large distance emphasis¶
MB4I
This feature emphasises large distances. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 1.21 | — | strong |
| dig. phantom | 2.5D | 1.33 | — | moderate |
| dig. phantom | 3D | 1 | — | very strong |
| config. A | 2D | 161 | 1 | moderate |
| config. A | 2.5D | 178 | 1 | moderate |
| config. B | 2D | 31.6 | 0.2 | moderate |
| config. B | 2.5D | 34.3 | 0.2 | moderate |
| config. C | 3D | 11 | 0.3 | strong |
| config. D | 3D | 10.3 | 0.1 | strong |
| config. E | 3D | 12.6 | 0.1 | moderate |
Low grey level zone emphasis¶
S1RA
This feature is a grey level analogue to small distance emphasis. Instead of small zone distances, low grey levels are emphasised. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.371 | — | strong |
| dig. phantom | 2.5D | 0.368 | — | moderate |
| dig. phantom | 3D | 0.253 | — | very strong |
| config. A | 2D | 0.0368 | 0.0005 | strong |
| config. A | 2.5D | 0.0291 | 0.0005 | strong |
| config. B | 2D | 0.0475 | 0.001 | strong |
| config. B | 2.5D | 0.0387 | 0.001 | strong |
| config. C | 3D | 0.00235 | \(6 \times 10^{-5}\) | strong |
| config. D | 3D | 0.0409 | 0.0005 | strong |
| config. E | 3D | 0.034 | 0.0004 | moderate |
High grey level zone emphasis¶
K26C
The high grey level zone emphasis feature is a grey level analogue to large distance emphasis. The feature emphasises high grey levels, and is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 16.4 | — | strong |
| dig. phantom | 2.5D | 16.2 | — | moderate |
| dig. phantom | 3D | 15.6 | — | very strong |
| config. A | 2D | 363 | 3 | strong |
| config. A | 2.5D | 370 | 3 | strong |
| config. B | 2D | 284 | 11 | strong |
| config. B | 2.5D | 284 | 11 | strong |
| config. C | 3D | 971 | 7 | strong |
| config. D | 3D | 188 | 10 | strong |
| config. E | 3D | 286 | 6 | strong |
Small distance low grey level emphasis¶
RUVG
This feature emphasises runs in the upper left quadrant of the GLDZM, where small zone distances and low grey levels are located. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.367 | — | strong |
| dig. phantom | 2.5D | 0.362 | — | moderate |
| dig. phantom | 3D | 0.253 | — | very strong |
| config. A | 2D | 0.00913 | 0.00023 | strong |
| config. A | 2.5D | 0.00788 | 0.00022 | strong |
| config. B | 2D | 0.0192 | 0.0005 | strong |
| config. B | 2.5D | 0.0168 | 0.0005 | strong |
| config. C | 3D | 0.00149 | \(4 \times 10^{-5}\) | strong |
| config. D | 3D | 0.0302 | 0.0006 | strong |
| config. E | 3D | 0.0228 | 0.0003 | moderate |
Small distance high grey level emphasis¶
DKNJ
This feature emphasises runs in the lower left quadrant of the GLDZM, where small zone distances and high grey levels are located. Small distance high grey level emphasis is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 15.2 | — | strong |
| dig. phantom | 2.5D | 14.3 | — | moderate |
| dig. phantom | 3D | 15.6 | — | very strong |
| config. A | 2D | 60.1 | 3.3 | strong |
| config. A | 2.5D | 49.5 | 2.8 | strong |
| config. B | 2D | 95.7 | 5.5 | strong |
| config. B | 2.5D | 81.4 | 4.6 | strong |
| config. C | 3D | 476 | 11 | strong |
| config. D | 3D | 99.3 | 5.1 | strong |
| config. E | 3D | 136 | 4 | moderate |
Large distance low grey level emphasis¶
A7WM
This feature emphasises runs in the upper right quadrant of the GLDZM, where large zone distances and low grey levels are located. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.386 | — | strong |
| dig. phantom | 2.5D | 0.391 | — | moderate |
| dig. phantom | 3D | 0.253 | — | very strong |
| config. A | 2D | 2.96 | 0.02 | moderate |
| config. A | 2.5D | 2.31 | 0.01 | moderate |
| config. B | 2D | 0.934 | 0.018 | moderate |
| config. B | 2.5D | 0.748 | 0.017 | moderate |
| config. C | 3D | 0.0154 | 0.0005 | strong |
| config. D | 3D | 0.183 | 0.004 | strong |
| config. E | 3D | 0.179 | 0.004 | moderate |
Large distance high grey level emphasis¶
KLTH
This feature emphasises runs in the lower right quadrant of the GLDZM, where large zone distances and high grey levels are located. The large distance high grey level emphasis feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 21.3 | — | strong |
| dig. phantom | 2.5D | 23.7 | — | moderate |
| dig. phantom | 3D | 15.6 | — | very strong |
| config. A | 2D | \(7.01 \times 10^{4}\) | 100 | moderate |
| config. A | 2.5D | \(7.95 \times 10^{4}\) | 100 | moderate |
| config. B | 2D | \(1.06 \times 10^{4}\) | 300 | strong |
| config. B | 2.5D | \(1.16 \times 10^{4}\) | 400 | strong |
| config. C | 3D | \(1.34 \times 10^{4}\) | 200 | strong |
| config. D | 3D | \(2.62 \times 10^{3}\) | 110 | strong |
| config. E | 3D | \(4.85 \times 10^{3}\) | 60 | moderate |
Grey level non-uniformity¶
VFT7
This feature measures the distribution of zone counts over the grey values. Grey level non-uniformity is low when zone counts are equally distributed along grey levels. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 1.41 | — | strong |
| dig. phantom | 2.5D | 5.44 | — | moderate |
| dig. phantom | 3D | 1.4 | — | very strong |
| config. A | 2D | 82.2 | 0.1 | strong |
| config. A | 2.5D | \(1.8 \times 10^{3}\) | 10 | strong |
| config. B | 2D | 20.5 | 0.1 | strong |
| config. B | 2.5D | 437 | 3 | strong |
| config. C | 3D | 195 | 6 | strong |
| config. D | 3D | 212 | 6 | strong |
| config. E | 3D | 231 | 6 | moderate |
Normalised grey level non-uniformity¶
7HP3
This is a normalised version of the grey level non-uniformity feature. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.323 | — | strong |
| dig. phantom | 2.5D | 0.302 | — | moderate |
| dig. phantom | 3D | 0.28 | — | very strong |
| config. A | 2D | 0.0728 | 0.0014 | strong |
| config. A | 2.5D | 0.0622 | 0.0007 | strong |
| config. B | 2D | 0.0789 | 0.001 | strong |
| config. B | 2.5D | 0.0613 | 0.0005 | strong |
| config. C | 3D | 0.0286 | 0.0003 | strong |
| config. D | 3D | 0.0491 | 0.0008 | strong |
| config. E | 3D | 0.0414 | 0.0003 | moderate |
Zone distance non-uniformity¶
V294
Zone distance non-uniformity measures the distribution of zone counts over the different zone distances. Zone distance non-uniformity is low when zone counts are equally distributed along zone distances. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 3.79 | — | strong |
| dig. phantom | 2.5D | 14.4 | — | moderate |
| dig. phantom | 3D | 5 | — | very strong |
| config. A | 2D | 64 | 0.4 | moderate |
| config. A | 2.5D | \(1.57 \times 10^{3}\) | 10 | strong |
| config. B | 2D | 39.8 | 0.3 | moderate |
| config. B | 2.5D | 963 | 6 | moderate |
| config. C | 3D | \(1.87 \times 10^{3}\) | 40 | strong |
| config. D | 3D | \(1.37 \times 10^{3}\) | 20 | strong |
| config. E | 3D | \(1.5 \times 10^{3}\) | 30 | moderate |
Normalised zone distance non-uniformity¶
IATH
This is a normalised version of the zone distance non-uniformity feature. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.898 | — | strong |
| dig. phantom | 2.5D | 0.802 | — | moderate |
| dig. phantom | 3D | 1 | — | very strong |
| config. A | 2D | 0.0716 | 0.0022 | strong |
| config. A | 2.5D | 0.0543 | 0.0014 | strong |
| config. B | 2D | 0.174 | 0.003 | strong |
| config. B | 2.5D | 0.135 | 0.001 | strong |
| config. C | 3D | 0.274 | 0.005 | strong |
| config. D | 3D | 0.317 | 0.004 | strong |
| config. E | 3D | 0.269 | 0.003 | moderate |
Zone percentage¶
VIWW
This feature measures the fraction of the number of realised zones and the maximum number of potential zones. Highly uniform ROIs produce a low zone percentage. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.24 | — | strong |
| dig. phantom | 2.5D | 0.243 | — | moderate |
| dig. phantom | 3D | 0.0676 | — | very strong |
| config. A | 2D | 0.3 | 0.003 | strong |
| config. A | 2.5D | 0.253 | 0.004 | moderate |
| config. B | 2D | 0.324 | 0.001 | strong |
| config. B | 2.5D | 0.26 | 0.002 | moderate |
| config. C | 3D | 0.148 | 0.003 | strong |
| config. D | 3D | 0.0972 | 0.0007 | strong |
| config. E | 3D | 0.126 | 0.001 | moderate |
Grey level variance¶
QK93
This feature estimates the variance in zone counts over the grey levels. Let \(p_{ij} = d_{ij}/N_s\) be the joint probability estimate for finding zones with discretised grey level \(i\) at distance \(j\). The feature is then defined as:
Here, \(\mu = \sum_{i=1}^{N_g} \sum_{j=1}^{N_d} i\,p_{ij}\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 3.97 | — | strong |
| dig. phantom | 2.5D | 3.92 | — | moderate |
| dig. phantom | 3D | 2.64 | — | very strong |
| config. A | 2D | 42.7 | 0.7 | moderate |
| config. A | 2.5D | 47.9 | 0.4 | strong |
| config. B | 2D | 36.1 | 0.3 | moderate |
| config. B | 2.5D | 41 | 0.7 | strong |
| config. C | 3D | 106 | 1 | strong |
| config. D | 3D | 32.7 | 1.6 | strong |
| config. E | 3D | 50.8 | 0.9 | strong |
Zone distance variance¶
7WT1
This feature estimates the variance in zone counts for the different zone distances. As before let \(p_{ij} = d_{ij}/N_s\). The feature is defined as:
Mean zone size is defined as \(\mu = \sum_{i=1}^{N_g} \sum_{j=1}^{N_d} j\,p_{ij}\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.051 | — | strong |
| dig. phantom | 2.5D | 0.0988 | — | moderate |
| dig. phantom | 3D | 0 | — | very strong |
| config. A | 2D | 69.4 | 0.1 | moderate |
| config. A | 2.5D | 78.9 | 0.1 | moderate |
| config. B | 2D | 13.5 | 0.1 | moderate |
| config. B | 2.5D | 15 | 0.1 | moderate |
| config. C | 3D | 4.6 | 0.06 | strong |
| config. D | 3D | 4.61 | 0.04 | strong |
| config. E | 3D | 5.56 | 0.05 | strong |
Zone distance entropy¶
GBDU
Again, let \(p_{ij} = d_{ij}/N_s\). Zone distance entropy is then defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 1.73 | — | strong |
| dig. phantom | 2.5D | 2 | — | moderate |
| dig. phantom | 3D | 1.92 | — | very strong |
| config. A | 2D | 8 | 0.04 | strong |
| config. A | 2.5D | 8.87 | 0.03 | strong |
| config. B | 2D | 6.47 | 0.03 | strong |
| config. B | 2.5D | 7.58 | 0.01 | moderate |
| config. C | 3D | 7.56 | 0.03 | strong |
| config. D | 3D | 6.61 | 0.03 | strong |
| config. E | 3D | 7.06 | 0.01 | moderate |
Neighbourhood grey tone difference based features¶
IPET
[Amadasun1989] introduced an alternative to the grey level co-occurrence matrix. The neighbourhood grey tone difference matrix (NGTDM) contains the sum of grey level differences of pixels/voxels with discretised grey level \(i\) and the average discretised grey level of neighbouring pixels/voxels within a Chebyshev distance \(\delta\). For 3D volumes, we can extend the original definition by Amadasun and King. Let \(X_{d,k}\) be the discretised grey level of a voxel at position \(\mathbf{k}=(k_x,k_y,k_z)\). Then the average grey level within a neighbourhood centred at \((k_x,k_y,k_z)\), but excluding \((k_x,k_y,k_z)\) itself is:
\(W=(2\delta+1)^3-1\) is the size of the 3D neighbourhood. For 2D \(W=(2\delta+1)^2-1\), and averages are not calculated between different slices. Neighbourhood grey tone difference \(s_i\) for discretised grey level \(i\) is then:
Here, \([\ldots]\) is an Iverson bracket, which is \(1\) if the conditions that the grey level \(X_{d,k}\) of voxel \(k\) is equal to \(i\) and the voxel has a valid neighbourhood are both true; it is \(0\) otherwise. \(N_v\) is the number of voxels in the ROI intensity mask.
A 2D example is shown in Fig. 18. A distance of \(\delta=1\) is used in this example, leading to 8 neighbouring pixels. Entry \(s_1=0\) because there are no valid pixels with grey level \(1\). Two pixels have grey level \(2\). The average value of their neighbours are \(19/8\) and \(21/8\). Thus \(s_2=|2-19/8|+|2-21/8|=1\). Similarly \(s_3=|3-19/8|=0.625\) and \(s_4=|4-17/8|=1.825\).
We deviate from the original definition by [Amadasun1989] as we do not demand that valid neighbourhoods are completely inside the ROI. In an irregular ROI mask, valid neighbourhoods may simply not exist for a distance \(\delta\). Instead, we consider a valid neighbourhood to exist if there is at least one neighbouring voxel included in the ROI mask. The average grey level for voxel \(k\) within a valid neighbourhood is then:
The neighbourhood size \(W_k\) for this voxel is equal to the number of voxels in the neighbourhood that are part of the ROI mask:
Under our definition, neighbourhood grey tone difference \(s_i\) for discretised grey level \(i\) can be directly expressed using neighbourhood size \(W_k\) of voxel \(k\):
Consequentially, \(n_i\) is the total number of voxels with grey level \(i\) which have a non-zero neighbourhood size.
Many NGTDM-based features depend on the \(N_g\) grey level probabilities \(p_i=n_i/N_{v,c}\), where \(N_g\) is the number of discretised grey levels in the ROI intensity mask and \(N_{v,c}=\sum n_i\) is total number of voxels that have at least one neighbour. If all voxels have at least one neighbour \(N_{v,c}=N_v\). Furthermore, let \(N_{g,p} \leq N_g\) be the number of discretised grey levels with \(p_i>0\). In the above example, \(N_g=4\) and \(N_{g,p}=3\).

Fig. 18 Original image with grey levels (a) and corresponding neighbourhood grey tone difference matrix (NGTDM) (b). The \(N_{v,c}\) pixels with valid neighbours at distance 1 are located within the rectangle in (a). The grey level voxel count \(n_i\), the grey level probability \(p_i=n_i/N_{v,c}\), and the neighbourhood grey level difference \(s_i\) for pixels with grey level \(i\) are included in the NGTDM. Note that our actual definition deviates from the original definition of [Amadasun1989], which is used here. In our definition complete neighbourhood are no longer required. In our definition the NGTDM would be calculated on the entire pixel area, and not solely on those pixels within the rectangle of panel (a).
Aggregating features¶
Three methods can be used to aggregate NGTDMs and arrive at a single feature value. A schematic example was previously shown in Fig. 16. A feature may be aggregated as follows:
- Features are computed from 2D matrices and averaged over slices (8QNN).
- The feature is computed from a single matrix after merging all 2D matrices (62GR).
- The feature is computed from a 3D matrix (KOBO).
Method 2 involves merging NGTDMs by summing the neighbourhood grey tone difference \(s_i\) and the number of voxels with a valid neighbourhood \(n_i\) and grey level \(i\) for NGTDMs of the different slices. Note that when NGTDMs are merged, \(N_{v,c}\) and \(p_i\) should be updated based on the merged NGTDM. Feature values may dependent strongly on the aggregation method.
Distances and distance weighting¶
The default neighbourhood is defined using the Chebyshev norm. Manhattan or Euclidean norms may be used as well. This requires a more general definition for the average grey level \(\overline{X}_k\):
The neighbourhood size \(W_k\) is:
As before, \(\big[\ldots\big]\) is an Iverson bracket.
Distance weighting for NGTDM is relatively straightforward. Let \(w\) be a weight dependent on \(\mathbf{m}\), e.g. \(w=\|\mathbf{m}\|^{-1}\) or \(w=\exp(-\|\mathbf{m}\|^2)\). The average grey level is then:
The neighbourhood size \(W_k\) becomes a general weight:
Employing different distance norms and distance weighting is considered non-standard use, and we caution against them due to potential reproducibility issues.
Coarseness¶
QCDE
Grey level differences in coarse textures are generally small due to large-scale patterns. Summing differences gives an indication of the level of the spatial rate of change in intensity [Amadasun1989]. Coarseness is defined as:
Because \(\sum_{i=1}^{N_g} p_i\,s_i\) potentially evaluates to 0, the maximum coarseness value is set to an arbitrary number of \(10^6\). Amadasun and King originally circumvented this issue by adding a unspecified small number \(\epsilon\) to the denominator, but an explicit, though arbitrary, maximum value should allow for more consistency.
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.121 | — | strong |
| dig. phantom | 2.5D | 0.0285 | — | strong |
| dig. phantom | 3D | 0.0296 | — | very strong |
| config. A | 2D | 0.00629 | 0.00046 | strong |
| config. A | 2.5D | \(9.06 \times 10^{-5}\) | \(3.3 \times 10^{-6}\) | strong |
| config. B | 2D | 0.0168 | 0.0005 | strong |
| config. B | 2.5D | 0.000314 | \(4 \times 10^{-6}\) | strong |
| config. C | 3D | 0.000216 | \(4 \times 10^{-6}\) | strong |
| config. D | 3D | 0.000208 | \(4 \times 10^{-6}\) | very strong |
| config. E | 3D | 0.000188 | \(4 \times 10^{-6}\) | strong |
Contrast¶
65HE
Contrast depends on the dynamic range of the grey levels as well as the spatial frequency of intensity changes [Amadasun1989]. Thus, contrast is defined as:
Grey level probabilities \(p_{i_{1}}\) and \(p_{i_{2}}\) are copies of \(p_i\) with different iterators, i.e. \(p_{i_{1}}=p_{i_{2}}\) for \(i_{1}=i_{2}\). The first term considers the grey level dynamic range, whereas the second term is a measure for intensity changes within the volume. If \(N_{g,p}=1\), \(F_{\mathit{ngt.contrast}}=0\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.925 | — | strong |
| dig. phantom | 2.5D | 0.601 | — | strong |
| dig. phantom | 3D | 0.584 | — | very strong |
| config. A | 2D | 0.107 | 0.002 | strong |
| config. A | 2.5D | 0.0345 | 0.0009 | strong |
| config. B | 2D | 0.181 | 0.001 | strong |
| config. B | 2.5D | 0.0506 | 0.0005 | strong |
| config. C | 3D | 0.0873 | 0.0019 | strong |
| config. D | 3D | 0.046 | 0.0005 | strong |
| config. E | 3D | 0.0752 | 0.0019 | strong |
Busyness¶
NQ30
Textures with large changes in grey levels between neighbouring voxels are said to be busy [Amadasun1989]. Busyness was defined as:
As before, \(p_{i_{1}}=p_{i_{2}}\) for \(i_{1}=i_{2}\). The original definition was erroneously formulated as the denominator will always evaluate to 0. Therefore we use a slightly different definition [Hatt2016]:
If \(N_{g,p}=1\), \(F_{\mathit{ngt.busyness}}=0\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 2.99 | — | strong |
| dig. phantom | 2.5D | 6.8 | — | strong |
| dig. phantom | 3D | 6.54 | — | very strong |
| config. A | 2D | 0.489 | 0.001 | strong |
| config. A | 2.5D | 8.84 | 0.01 | strong |
| config. B | 2D | 0.2 | 0.005 | strong |
| config. B | 2.5D | 3.45 | 0.07 | strong |
| config. C | 3D | 1.39 | 0.01 | strong |
| config. D | 3D | 5.14 | 0.14 | very strong |
| config. E | 3D | 4.65 | 0.1 | strong |
Complexity¶
HDEZ
Complex textures are non-uniform and rapid changes in grey levels are common [Amadasun1989]. Texture complexity is defined as:
As before, \(p_{i_{1}}=p_{i_{2}}\) for \(i_{1}=i_{2}\), and likewise \(s_{i_{1}}=s_{i_{2}}\) for \(i_{1}=i_{2}\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 10.4 | — | strong |
| dig. phantom | 2.5D | 14.1 | — | strong |
| dig. phantom | 3D | 13.5 | — | very strong |
| config. A | 2D | 438 | 9 | strong |
| config. A | 2.5D | 580 | 19 | strong |
| config. B | 2D | 391 | 7 | strong |
| config. B | 2.5D | 496 | 5 | strong |
| config. C | 3D | \(1.81 \times 10^{3}\) | 60 | strong |
| config. D | 3D | 400 | 5 | strong |
| config. E | 3D | 574 | 1 | strong |
Strength¶
1X9X
[Amadasun1989] defined texture strength as:
As before, \(p_{i_{1}}=p_{i_{2}}\) for \(i_{1}=i_{2}\). If \(\sum_{i=1}^{N_g}s_i=0\), \(F_{\mathit{ngt.strength}}=0\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 2.88 | — | strong |
| dig. phantom | 2.5D | 0.741 | — | strong |
| dig. phantom | 3D | 0.763 | — | very strong |
| config. A | 2D | 3.33 | 0.08 | strong |
| config. A | 2.5D | 0.0904 | 0.0027 | strong |
| config. B | 2D | 6.02 | 0.23 | strong |
| config. B | 2.5D | 0.199 | 0.009 | strong |
| config. C | 3D | 0.651 | 0.015 | strong |
| config. D | 3D | 0.162 | 0.008 | very strong |
| config. E | 3D | 0.167 | 0.006 | strong |
Neighbouring grey level dependence based features¶
REK0
[Sun1983] defined the neighbouring grey level dependence matrix (NGLDM) as an alternative to the grey level co-occurrence matrix. The NGLDM aims to capture the coarseness of the overall texture and is rotationally invariant.
NGLDM also involves the concept of a neighbourhood around a central voxel. All voxels within Chebyshev distance \(\delta\) are considered to belong to the neighbourhood of the center voxel. The discretised grey levels of the center voxel \(k\) at position \(\mathbf{k}\) and a neighbouring voxel \(m\) at \(\mathbf{k}+\mathbf{m}\) are said to be dependent if \(|X_d(\mathbf{k}) - X_d(\mathbf{k}+\mathbf{m}) | \leq \alpha\), with \(\alpha\) being a non-negative integer coarseness parameter. The number of grey level dependent voxels \(j\) within the neighbourhood is then counted as:
Here, \(\big[\ldots\big]\) is an Iverson bracket, which is \(1\) if the aforementioned condition is fulfilled, and \(0\) otherwise. Note that the minimum dependence \(j_k=1\) and not \(j_k=0\). This is done because some feature definitions require a minimum dependence of 1 or are undefined otherwise. One may therefore also simplify the expression for \(j_k\) by including the center voxel:
Dependence \(j_k\) is iteratively determined for each voxel \(k\) in the ROI intensity mask. \(\mathbf{M}\) is then the \(N_g \times N_n\) neighbouring grey level dependence matrix, where \(N_g\) is the number of discretised grey levels present in the ROI intensity mask and \(N_n=\text{max}(j_k)\) the maximum grey level dependence count found. Element \(s_{ij}\) of \(\mathbf{M}\) is then the number of neighbourhoods with a center voxel with discretised grey level \(i\) and a neighbouring voxel dependence \(j\). Furthermore, let \(N_v\) be the number of voxels in the ROI intensity mask, and \(N_s = \sum_{i=1}^{N_g}\sum_{j=1}^{N_n} s_{ij}\) the number of neighbourhoods. Marginal sums can likewise be defined. Let \(s_{i.}=\sum_{j=1}^{N_n}\) be the number of neighbourhoods with discretised grey level \(i\), and let \(s_{j.}=\sum_{i=1}^{N_g}s_{ij}\) be the number of neighbourhoods with dependence \(j\), regardless of grey level. A two dimensional example is shown in Fig. 19.
The definition we actually use deviates from the original by [Sun1983]. Because regions of interest are rarely cuboid, omission of neighbourhoods which contain voxels outside the ROI mask may lead to inconsistent results, especially for larger distance \(\delta\). Hence the neighbourhoods of all voxels in the within the ROI intensity mask are considered, and consequently \(N_v=N_s\). Neighbourhood voxels located outside the ROI do not add to dependence \(j\):
Note that while \(\alpha=0\) is a typical choice for the coarseness parameter, different \(\alpha\) are possible. Likewise, a typical choice for neighbourhood radius \(\delta\) is Chebyshev distance \(\delta=1\) but larger values are possible as well.
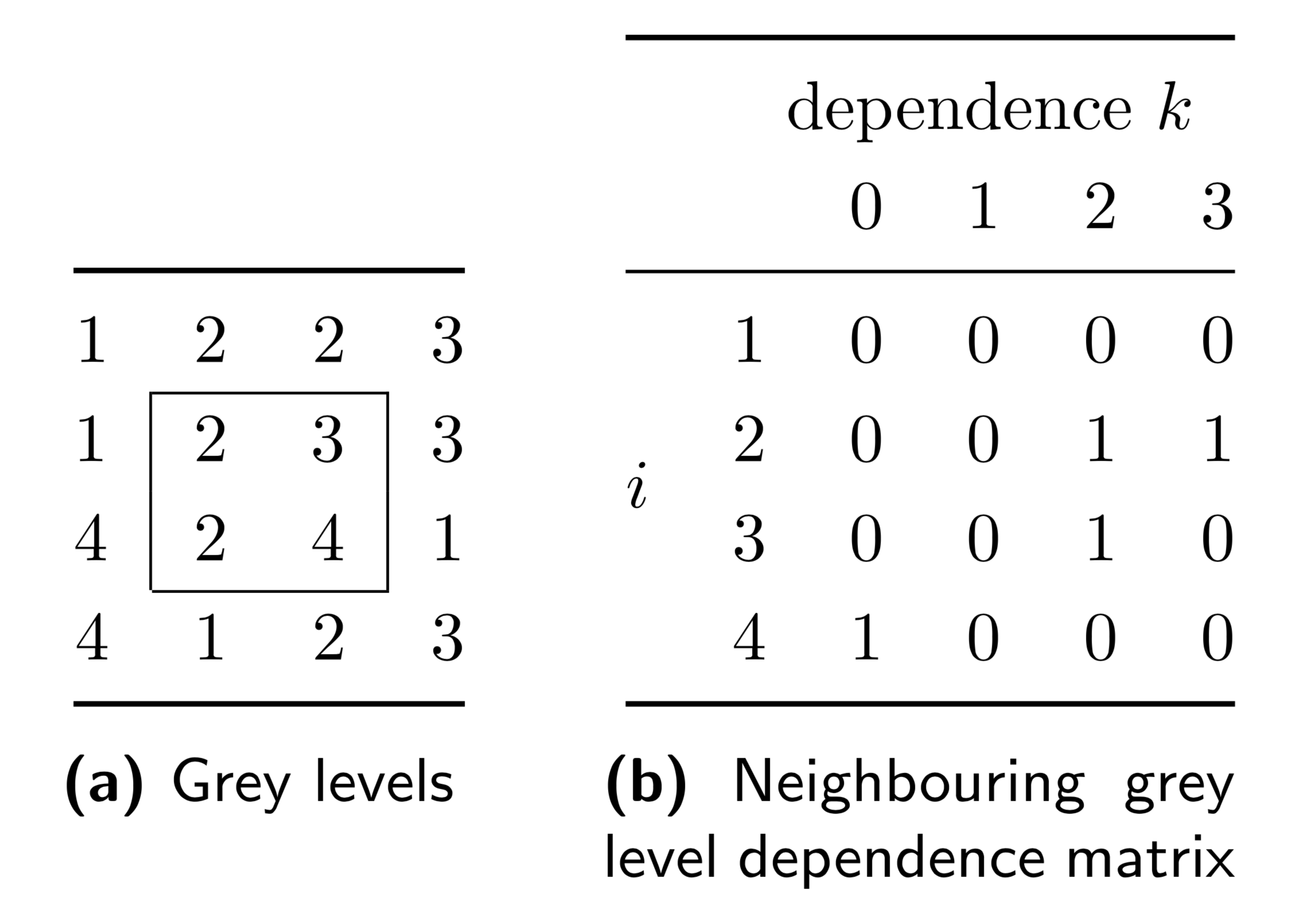
Fig. 19 Original image with grey levels and pixels with a complete neighbourhood within the square (a); corresponding neighbouring grey level dependence matrix for distance \(d = \sqrt{2}\) and coarseness parameter \(a = 0\) (b). Element \(s_{i,j}\) of the NGLDM indicates the number of neighbourhoods with a center pixel with grey level i and neighbouring grey level dependence k within the image. Note that in our definition a complete neighbourhood is no longer required. Thus every voxel is considered as a center voxel with a neighbourhood, instead of being constrained to the voxels within the square in panel (a).
Aggregating features¶
Three methods can be used to aggregate NGLDMs and arrive at a single feature value. A schematic example was previously shown in Fig. 16. A feature may be aggregated as follows:
- Features are computed from 2D matrices and averaged over slices (8QNN).
- The feature is computed from a single matrix after merging all 2D matrices (62GR).
- The feature is computed from a 3D matrix (KOBO).
Method 2 involves merging NGLDMs by summing the dependence count \(s_{ij}\) by element over the NGLDM of the different slices. Note that when NGLDMs are merged, \(N_v\) and \(N_s\) should likewise be summed to retain consistency. Feature values may dependent strongly on the aggregation method.
Distances and distance weighting¶
Default neighbourhoods are constructed using the Chebyshev norm, but other norms can be used as well. For this purpose it is useful to generalise the dependence count equation to:
with \(\mathbf{m}\) the vector between voxels \(k\) and \(m\) and \(\|\mathbf{m}\|\) its length according to the particular norm.
In addition, dependence may be weighted by distance. Let \(w\) be a weight dependent on \(\mathbf{m}\), e.g. \(w=\|\mathbf{m}\|^{-1}\) or \(w=\exp(-\|\mathbf{m}\|^2)\). The dependence of voxel \(k\) is then:
Employing different distance norms and distance weighting is considered non-standard use, and we caution against them due to potential reproducibility issues.
Note on feature references¶
The NGLDM is structured similarly to the GLRLM, GLSZM and GLDZM. NGLDM feature definitions are therefore based on the definitions of GLRLM features, and references may be found in Grey level run length based features, except for the features originally defined by [Sun1983].
Low dependence emphasis¶
SODN
This feature emphasises low neighbouring grey level dependence counts. [Sun1983] refer to this feature as small number emphasis. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.158 | — | strong |
| dig. phantom | 2.5D | 0.159 | — | strong |
| dig. phantom | 3D | 0.045 | — | very strong |
| config. A | 2D | 0.281 | 0.003 | strong |
| config. A | 2.5D | 0.243 | 0.004 | strong |
| config. B | 2D | 0.31 | 0.001 | strong |
| config. B | 2.5D | 0.254 | 0.002 | strong |
| config. C | 3D | 0.137 | 0.003 | strong |
| config. D | 3D | 0.0912 | 0.0007 | strong |
| config. E | 3D | 0.118 | 0.001 | strong |
High dependence emphasis¶
IMOQ
This feature emphasises high neighbouring grey level dependence counts. [Sun1983] refer to this feature as large number emphasis. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 19.2 | — | strong |
| dig. phantom | 2.5D | 18.8 | — | strong |
| dig. phantom | 3D | 109 | — | very strong |
| config. A | 2D | 14.8 | 0.1 | strong |
| config. A | 2.5D | 16.1 | 0.2 | strong |
| config. B | 2D | 17.3 | 0.2 | strong |
| config. B | 2.5D | 19.6 | 0.2 | strong |
| config. C | 3D | 126 | 2 | strong |
| config. D | 3D | 223 | 5 | strong |
| config. E | 3D | 134 | 3 | strong |
Low grey level count emphasis¶
TL9H
This feature is a grey level analogue to low dependence emphasis. Instead of low neighbouring grey level dependence counts, low grey levels are emphasised. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.702 | — | strong |
| dig. phantom | 2.5D | 0.693 | — | strong |
| dig. phantom | 3D | 0.693 | — | very strong |
| config. A | 2D | 0.0233 | 0.0003 | strong |
| config. A | 2.5D | 0.0115 | 0.0003 | strong |
| config. B | 2D | 0.0286 | 0.0004 | strong |
| config. B | 2.5D | 0.0139 | 0.0005 | strong |
| config. C | 3D | 0.0013 | \(4 \times 10^{-5}\) | strong |
| config. D | 3D | 0.0168 | 0.0009 | strong |
| config. E | 3D | 0.0154 | 0.0007 | strong |
High grey level count emphasis¶
OAE7
The high grey level count emphasis feature is a grey level analogue to high dependence emphasis. The feature emphasises high grey levels, and is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 7.49 | — | strong |
| dig. phantom | 2.5D | 7.66 | — | strong |
| dig. phantom | 3D | 7.66 | — | very strong |
| config. A | 2D | 446 | 2 | strong |
| config. A | 2.5D | 466 | 2 | strong |
| config. B | 2D | 359 | 10 | strong |
| config. B | 2.5D | 375 | 11 | strong |
| config. C | 3D | \(1.57 \times 10^{3}\) | 10 | strong |
| config. D | 3D | 364 | 16 | strong |
| config. E | 3D | 502 | 8 | strong |
Low dependence low grey level emphasis¶
EQ3F
This feature emphasises neighbouring grey level dependence counts in the upper left quadrant of the NGLDM, where low dependence counts and low grey levels are located. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.0473 | — | strong |
| dig. phantom | 2.5D | 0.0477 | — | strong |
| dig. phantom | 3D | 0.00963 | — | very strong |
| config. A | 2D | 0.0137 | 0.0002 | strong |
| config. A | 2.5D | 0.00664 | 0.0002 | strong |
| config. B | 2D | 0.0203 | 0.0003 | strong |
| config. B | 2.5D | 0.00929 | 0.00026 | strong |
| config. C | 3D | 0.000306 | \(1.2 \times 10^{-5}\) | strong |
| config. D | 3D | 0.00357 | \(4 \times 10^{-5}\) | strong |
| config. E | 3D | 0.00388 | \(4 \times 10^{-5}\) | strong |
Low dependence high grey level emphasis¶
JA6D
This feature emphasises neighbouring grey level dependence counts in the lower left quadrant of the NGLDM, where low dependence counts and high grey levels are located. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 3.06 | — | strong |
| dig. phantom | 2.5D | 3.07 | — | strong |
| dig. phantom | 3D | 0.736 | — | very strong |
| config. A | 2D | 94.2 | 0.4 | strong |
| config. A | 2.5D | 91.9 | 0.5 | strong |
| config. B | 2D | 78.9 | 2.2 | strong |
| config. B | 2.5D | 73.4 | 2.1 | strong |
| config. C | 3D | 141 | 2 | strong |
| config. D | 3D | 18.9 | 1.1 | strong |
| config. E | 3D | 36.7 | 0.5 | strong |
High dependence low grey level emphasis¶
NBZI
This feature emphasises neighbouring grey level dependence counts in the upper right quadrant of the NGLDM, where high dependence counts and low grey levels are located. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 17.6 | — | strong |
| dig. phantom | 2.5D | 17.2 | — | strong |
| dig. phantom | 3D | 102 | — | very strong |
| config. A | 2D | 0.116 | 0.001 | strong |
| config. A | 2.5D | 0.0674 | 0.0004 | strong |
| config. B | 2D | 0.108 | 0.003 | strong |
| config. B | 2.5D | 0.077 | 0.0019 | strong |
| config. C | 3D | 0.0828 | 0.0003 | strong |
| config. D | 3D | 0.798 | 0.072 | strong |
| config. E | 3D | 0.457 | 0.031 | strong |
High dependence high grey level emphasis¶
9QMG
The high dependence high grey level emphasis feature emphasises neighbouring grey level dependence counts in the lower right quadrant of the NGLDM, where high dependence counts and high grey levels are located. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 49.5 | — | strong |
| dig. phantom | 2.5D | 50.8 | — | strong |
| dig. phantom | 3D | 235 | — | very strong |
| config. A | 2D | \(7.54 \times 10^{3}\) | 60 | strong |
| config. A | 2.5D | \(8.1 \times 10^{3}\) | 60 | strong |
| config. B | 2D | \(7.21 \times 10^{3}\) | 130 | strong |
| config. B | 2.5D | \(7.97 \times 10^{3}\) | 150 | strong |
| config. C | 3D | \(2.27 \times 10^{5}\) | \(3 \times 10^{3}\) | strong |
| config. D | 3D | \(9.28 \times 10^{4}\) | \(1.3 \times 10^{3}\) | strong |
| config. E | 3D | \(7.6 \times 10^{4}\) | 600 | strong |
Grey level non-uniformity¶
FP8K
Grey level non-uniformity assesses the distribution of neighbouring grey level dependence counts over the grey values. The feature value is low when dependence counts are equally distributed along grey levels. The feature is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 10.2 | — | strong |
| dig. phantom | 2.5D | 37.9 | — | strong |
| dig. phantom | 3D | 37.9 | — | very strong |
| config. A | 2D | 757 | 1 | strong |
| config. A | 2.5D | \(1.72 \times 10^{4}\) | 100 | strong |
| config. B | 2D | 216 | 3 | strong |
| config. B | 2.5D | \(4.76 \times 10^{3}\) | 50 | strong |
| config. C | 3D | \(6.42 \times 10^{3}\) | 10 | strong |
| config. D | 3D | \(1.02 \times 10^{4}\) | 300 | strong |
| config. E | 3D | \(8.17 \times 10^{3}\) | 130 | strong |
Normalised grey level non-uniformity¶
5SPA
This is a normalised version of the grey level non-uniformity feature. It is defined as:
The normalised grey level non-uniformity computed from a single 3D NGLDM matrix is equivalent to the intensity histogram uniformity feature [VanGriethuysen2017].
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.562 | — | strong |
| dig. phantom | 2.5D | 0.512 | — | strong |
| dig. phantom | 3D | 0.512 | — | very strong |
| config. A | 2D | 0.151 | 0.003 | strong |
| config. A | 2.5D | 0.15 | 0.002 | strong |
| config. B | 2D | 0.184 | 0.001 | strong |
| config. B | 2.5D | 0.174 | 0.001 | strong |
| config. C | 3D | 0.14 | 0.003 | strong |
| config. D | 3D | 0.229 | 0.003 | strong |
| config. E | 3D | 0.184 | 0.001 | strong |
Dependence count non-uniformity¶
Z87G
This features assesses the distribution of neighbouring grey level dependence counts over the different dependence counts. The feature value is low when dependence counts are equally distributed. [Sun1983] refer to this feature as number non-uniformity. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 3.96 | — | strong |
| dig. phantom | 2.5D | 12.4 | — | strong |
| dig. phantom | 3D | 4.86 | — | very strong |
| config. A | 2D | 709 | 2 | strong |
| config. A | 2.5D | \(1.75 \times 10^{4}\) | 100 | strong |
| config. B | 2D | 157 | 1 | strong |
| config. B | 2.5D | \(3.71 \times 10^{3}\) | 30 | strong |
| config. C | 3D | \(2.45 \times 10^{3}\) | 60 | strong |
| config. D | 3D | \(1.84 \times 10^{3}\) | 30 | strong |
| config. E | 3D | \(2.25 \times 10^{3}\) | 30 | strong |
Normalised dependence count non-uniformity¶
OKJI
This is a normalised version of the dependence count non-uniformity feature. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.212 | — | strong |
| dig. phantom | 2.5D | 0.167 | — | strong |
| dig. phantom | 3D | 0.0657 | — | very strong |
| config. A | 2D | 0.175 | 0.001 | strong |
| config. A | 2.5D | 0.153 | 0.001 | strong |
| config. B | 2D | 0.179 | 0.001 | strong |
| config. B | 2.5D | 0.136 | 0.001 | strong |
| config. C | 3D | 0.0532 | 0.0005 | strong |
| config. D | 3D | 0.0413 | 0.0003 | strong |
| config. E | 3D | 0.0505 | 0.0003 | strong |
Dependence count percentage¶
6XV8
This feature measures the fraction of the number of realised neighbourhoods and the maximum number of potential neighbourhoods. Dependence count percentage may be completely omitted as it evaluates to \(1\) when complete neighbourhoods are not required, as is the case under our definition. It is defined as:
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 1 | — | strong |
| dig. phantom | 2.5D | 1 | — | moderate |
| dig. phantom | 3D | 1 | — | strong |
| config. A | 2D | 1 | — | moderate |
| config. A | 2.5D | 1 | — | moderate |
| config. B | 2D | 1 | — | moderate |
| config. B | 2.5D | 1 | — | moderate |
| config. C | 3D | 1 | — | strong |
| config. D | 3D | 1 | — | strong |
| config. E | 3D | 1 | — | moderate |
Grey level variance¶
1PFV
This feature estimates the variance in dependence counts over the grey levels. Let \(p_{ij} = s_{ij}/N_s\) be the joint probability estimate for finding discretised grey level \(i\) with dependence \(j\). The feature is then defined as:
Here, \(\mu = \sum_{i=1}^{N_g} \sum_{j=1}^{N_n} i\,p_{ij}\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 2.7 | — | strong |
| dig. phantom | 2.5D | 3.05 | — | strong |
| dig. phantom | 3D | 3.05 | — | very strong |
| config. A | 2D | 31.1 | 0.5 | strong |
| config. A | 2.5D | 22.8 | 0.6 | strong |
| config. B | 2D | 25.3 | 0.4 | strong |
| config. B | 2.5D | 18.7 | 0.2 | strong |
| config. C | 3D | 81.1 | 2.1 | strong |
| config. D | 3D | 21.7 | 0.4 | strong |
| config. E | 3D | 30.4 | 0.8 | strong |
}
Dependence count variance¶
DNX2
This feature estimates the variance in dependence counts over the different possible dependence counts. As before let \(p_{ij} = s_{ij}/N_s\). The feature is defined as:
Mean dependence count is defined as \(\mu = \sum_{i=1}^{N_g} \sum_{j=1}^{N_n} j\,p_{ij}\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 2.73 | — | strong |
| dig. phantom | 2.5D | 3.27 | — | strong |
| dig. phantom | 3D | 22.1 | — | very strong |
| config. A | 2D | 3.12 | 0.02 | strong |
| config. A | 2.5D | 3.37 | 0.01 | strong |
| config. B | 2D | 4.02 | 0.05 | strong |
| config. B | 2.5D | 4.63 | 0.06 | strong |
| config. C | 3D | 39.2 | 0.1 | strong |
| config. D | 3D | 63.9 | 1.3 | strong |
| config. E | 3D | 39.4 | 1 | strong |
Dependence count entropy¶
FCBV
This feature is referred to as entropy by [Sun1983]. Let \(p_{ij} = s_{ij}/N_s\). Dependence count entropy is then defined as:
This definition remedies an error in the definition of [Sun1983], where the term within the logarithm is dependence count \(s_{ij}\) instead of count probability \(p_{ij}\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 2.71 | — | strong |
| dig. phantom | 2.5D | 3.36 | — | strong |
| dig. phantom | 3D | 4.4 | — | very strong |
| config. A | 2D | 5.76 | 0.02 | strong |
| config. A | 2.5D | 5.93 | 0.02 | strong |
| config. B | 2D | 5.38 | 0.01 | strong |
| config. B | 2.5D | 5.78 | 0.01 | strong |
| config. C | 3D | 7.54 | 0.03 | strong |
| config. D | 3D | 6.98 | 0.01 | strong |
| config. E | 3D | 7.06 | 0.02 | strong |
Dependence count energy¶
CAS9
This feature is called second moment by [Sun1983]. Let \(p_{ij} = s_{ij}/N_s\). Then dependence count energy is defined as:
This definition also remedies an error in the original definition, where squared dependence count \(s_{ij}^2\) is divided by \(N_s\) only, thus leaving a major volume dependency. In the definition given here, \(s_{ij}^2\) is normalised by \(N_s^2\) through the use of count probability \(p_{ij}\).
| data | aggr. method | value | tol. | consensus |
|---|---|---|---|---|
| dig. phantom | 2D | 0.17 | — | strong |
| dig. phantom | 2.5D | 0.122 | — | strong |
| dig. phantom | 3D | 0.0533 | — | very strong |
| config. A | 2D | 0.0268 | 0.0004 | strong |
| config. A | 2.5D | 0.0245 | 0.0003 | moderate |
| config. B | 2D | 0.0321 | 0.0002 | strong |
| config. B | 2.5D | 0.0253 | 0.0001 | moderate |
| config. C | 3D | 0.00789 | 0.00011 | strong |
| config. D | 3D | 0.0113 | 0.0002 | strong |
| config. E | 3D | 0.0106 | 0.0001 | strong |